
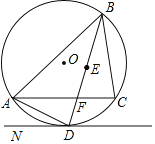
【题目】如图,⊙O是△ABC的外接圆,点E为△ABC内切圆的圆心,连接EB的延长线交AC于点F,交⊙O于点D,连接AD,过点D作直线DN,使∠ADN=∠DBC.
(1)求证:直线DN是⊙O的切线;
(2)若DF=1,且BF=3,求AD的长.
【答案】(1)证明见解析;(2)AD=![]() .
.
【解析】
(1)根据垂径定理的推论即可得到OD⊥AC,再根据∠ADN=∠DAC,即可判定AC∥DN,进而得到OD⊥DN,据此可得直线DN是⊙O的切线.
(2)根据三角形内心的定义以及圆周角定理,得到∠AED=∠EAD,即可得出DA=DE,再判定△DAF∽△DBA,即可得到DA2=DFDB,据此解答即可.
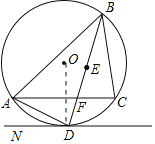
解: (1)证明:如图所示,连接OD,
∵点E是△ABC的内心,
∴∠ABD=∠CBD,
∴![]() ,
,
∴OD⊥BC,
又∵∠ADN=∠DBC,∠DBC=∠DAC,
∴∠ADN=∠DAC,
∴AC∥DN,
∴OD⊥DN,
又∵OD为⊙O半径,
∴直线DN是⊙O的切线;
(2)∵![]() ,
,
∴∠DAF=∠DBA,
又∵∠ADF=∠ADB(公共角),
∴△DAF∽△DBA,
∴![]() ,即DA2=DFDB,
,即DA2=DFDB,
∵DF=2,BF=3,
∴DB=DF+BF=5
∴DA2=DFDB=10
∴DA=DE=![]() .
.


 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有3个标记为1、2、-3的小球(材质、形状、大小等完全相同),甲先从中随机取出一个小球,记下数字为x后放回,同样的乙也从中随机取出一个小球,记下数字为y,这样确定了点P的坐标(x,y).
(1)请用列表或画树状图的方法写出点P所有可能的坐标;
(2)求点P在函数y=﹣x2+2的图象上的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于题目“一段抛物线L:y=﹣x(x﹣3)+c(0≤x≤3)与直线l:y=x+2有唯一公共点,若c为整数,确定所有c的值,”甲的结果是c=1,乙的结果是c=3或4,则( )
A. 甲的结果正确
B. 乙的结果正确
C. 甲、乙的结果合在一起才正确
D. 甲、乙的结果合在一起也不正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校5月份举行了八年级生物实验考查,有A和B两个考查实验,规定每位学生只参加其中一个实验的考查,并由学生自己抽签决定具体的考查实验,小明、小丽、小华都参加了本次考查.
(1)小丽参加实验A考查的概率是 ;
(2)用列表或画树状图的方法求小明、小丽都参加实验A考查的概率;
(3)他们三人都参加实验A考查的概率是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
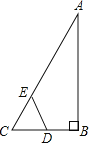
【题目】如图,Rt△ABC中,∠ABC=90°,∠ACB=60°,BC=4cm,D为BC的中点,若动点E以1cm/s的速度从点A出发,沿着A→C→A的方向运动,设点E的运动时间为秒(0≤t≤12),连接DE,当△CDE是直角三角形时,t的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
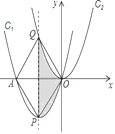
【题目】如图,在平面直角坐标系xOy中,抛物线C1:y1=![]() (x+3)2﹣
(x+3)2﹣![]() ,将抛物线C1 向右平移3个单位、再向上平移4.5个单位得抛物线C2,则图中阴影部分的面积为________.
,将抛物线C1 向右平移3个单位、再向上平移4.5个单位得抛物线C2,则图中阴影部分的面积为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于A(2,3),B两点,P是第一象限内的双曲线上在意一点,直线PA交x轴于点M,连接PB交x轴于点N,若∠APN = 90°,则PM的长为______.
相交于A(2,3),B两点,P是第一象限内的双曲线上在意一点,直线PA交x轴于点M,连接PB交x轴于点N,若∠APN = 90°,则PM的长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明和小丽所在生活小区的管理人员为了方便业主合理规范摆放机动车,在小区内部道路的一侧按照标准画出了一些停车位.
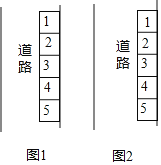
(1)如图1,小明家楼下的道路上有五个空停车位,标号分别为1,2,3,4,5,如果有一辆机动车要随机停在这五个停车位中的一个里边,则该机动车停在“标号是奇数”停车位的概率是 .
(2)如图2,小丽家楼下的道路上有四个空停车位,标号分别为1,2,3,4,如果有两辆机动车要随机停在这四个停车位中的两个里边,请用列表或画树状图的方法得出这两辆机动车停在“标号是一个奇数和一个偶数”停车位的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
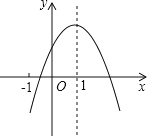
【题目】已知二次函数![]() 的图象如图所示,有下列5个结论:
的图象如图所示,有下列5个结论:
①abc<0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+b<m (am+b)(m≠1的实数).
其中正确结论的序号有 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com