
【题目】在平面直角坐标系xOy中,直线![]() 与双曲线
与双曲线![]() 相交于A(2,3),B两点,P是第一象限内的双曲线上在意一点,直线PA交x轴于点M,连接PB交x轴于点N,若∠APN = 90°,则PM的长为______.
相交于A(2,3),B两点,P是第一象限内的双曲线上在意一点,直线PA交x轴于点M,连接PB交x轴于点N,若∠APN = 90°,则PM的长为______.
【答案】![]()
【解析】
过P作直线PE⊥x轴于点E,过点A作AC⊥PE于点C,过点B作BD⊥PE于点D,先用待定系数法求出两个函数的解析式,再求得B点坐标,然后证明△ACP∽△PDB,运用相似三角形的性质列出关于t的方程,求得t的值,再求AP的解析式,进而求得PM的长.
解:过P作直线PE⊥x轴于点E,过点A作AC⊥PE于点C,过点B作BD⊥PE于点D,如图所示,
把A(2,3)代入y=kx中,得3=2k,
∴k=![]() ,
,
∴直线AB的解析式为:y=![]() x,
x,
把A(2,3)代入y=![]() 中,得m=6,
中,得m=6,
∴反比例函数的解析式为:y=![]() ,
,
根据反比例函数与正比例函数的对称性可得B(2,3),
设P点的坐标为(t,![]() ),
),
则AC=t2,PC=3![]() ,BD=t+2,PD=
,BD=t+2,PD=![]() +3,
+3,
∵∠ACP=∠BDP=90°,∠APN=90°,
∴∠CAP+∠APC=∠APC+∠BPD=90°,
∴∠CAP=∠BPD,
∴△ACP∽△PDB,
∴![]() ,即
,即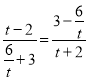 ,
,
解得,t=2(A点的横坐标),或t=3,
∴P(3,2),
设直线AP的解析式为:y=ax+b(a≠0),则![]() ,解得,
,解得,![]() ,
,
∴直线AP的解析式为:y=x+5,
令y=0,得x=5,
∴M(5,0),
∴PM=![]() =
=![]() ,
,
故答案为:![]() .
.



科目:初中数学 来源: 题型:
【题目】如图,△ABC是边长为2的等边三角形.取BC边中点E,作ED∥AB,EF∥AC,得到四边形EDAF,它的面积记作s1;取BE中点E1,作E1D1∥FB,E1F1∥EF,得到四边形E1D1FF1,它的面积记作s2.照此规律作下去,则s2019=_____.
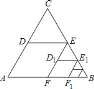
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=BC,CE∥AB,以AB为直径作⊙O,当CE是⊙O的切线时,切点为D.
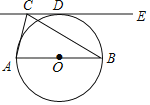
(1)求:∠ABC的度数;
(2)若CD=3,求AC的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
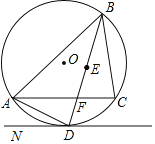
【题目】如图,⊙O是△ABC的外接圆,点E为△ABC内切圆的圆心,连接EB的延长线交AC于点F,交⊙O于点D,连接AD,过点D作直线DN,使∠ADN=∠DBC.
(1)求证:直线DN是⊙O的切线;
(2)若DF=1,且BF=3,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)在直角坐标系中画出二次函数y=![]() x2﹣x﹣
x2﹣x﹣![]() 的图象.
的图象.
(2)若将y=![]() x2﹣x﹣
x2﹣x﹣![]() 图象沿x轴向左平移2个单位,请写出平移后图象所对应的函数关系式.
图象沿x轴向左平移2个单位,请写出平移后图象所对应的函数关系式.
(3)根据图象,写出当y>0时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是根据九年级某班50名同学一周的锻炼情况绘制的条形统计图,下面关于该班50名同学一周锻炼时间的说法错误的是( )

A. 众数是7 B. 中位数是6.5
C. 平均数是 6.5 D. 平均每周锻炼超过6小时的人占总数的一半
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,ABCD是边长为1的正方形,O是正方形的中心,Q是边CD上一个动点(点Q不与点C、D重合),直线AQ与BC的延长线交于点E,AE交BD于点P.设DQ=x.
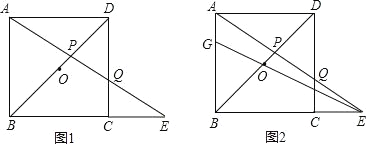
(1)填空:当![]() 时,
时,![]() 的值为 ;
的值为 ;
(2)如图2,直线EO交AB于点G,若BG=y,求y关于x之间的函数关系式;
(3)在第(2)小题的条件下,是否存在点Q,使得PG∥BC?若存在,求x的值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,三孔桥横截面的三个孔都呈抛物线形,两小孔形状、大小都相同.正常水位时,大孔水面宽度![]() 米,顶点
米,顶点![]() 距水面
距水面![]() 米(即
米(即![]() 米),小孔顶点
米),小孔顶点![]() 距水面
距水面![]() 米(即
米(即![]() 米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,则此时大孔的水面宽度
米).当水位上涨刚好淹没小孔时,借助图中的直角坐标系,则此时大孔的水面宽度![]() 长为( )
长为( )
![]()

A. ![]() 米 B.
米 B. ![]() C.
C. ![]() 米 D.
米 D. ![]() 米
米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=mx2﹣2mx﹣3(m≠0)与y轴交于点A,与x轴交于点B、C(B在C的左侧)
(1)求点A的坐标和对称轴
(2)若∠ACB=45°,求此抛物线的表达式;
(3)在(2)的条件下,对称轴上是否存在一点P,使△PAB的周长最小?若存在,求出P点坐标和△PAB的周长,若不存在,请说明理由。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com