
分析 (1)将点A的坐标代入反比例函数y1=$\frac{{k}_{1}}{x}$中,可求k1值,再把y=-3代入 反比例函数y1=$\frac{2}{x}$即可求得B的坐标,根据两函数图象的交点,图象的位置可确定y1<y2时x的范围.
解答 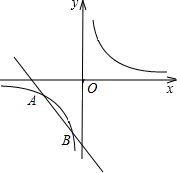 解:∵反比例函数y1=$\frac{{k}_{1}}{x}$与过点A(-2,-1),
解:∵反比例函数y1=$\frac{{k}_{1}}{x}$与过点A(-2,-1),
∴k1=-1×(-2)=2.
∵把y=-3代入 反比例函数y1=$\frac{2}{x}$,得-3=$\frac{2}{x}$,
解得x=-$\frac{2}{3}$.
∴B(-$\frac{2}{3}$,-3),
当x<-2或-$\frac{2}{3}$<x<0时,y1<y2.
故答案为x<-2或-$\frac{2}{3}$<x<0.
点评 本题主要考查了待定系数法求反比例函数的解析式和反比例函数y=$\frac{k}{x}$中k的几何意义.这里体现了数形结合的思想,做此类题一定要正确理解k的几何意义.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
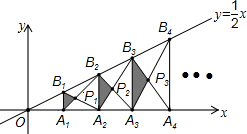 如图,已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=$\frac{1}{2}$x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn,△A1B1P1,△A2B2P2,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn=$\frac{{n}^{2}}{8n+4}$(请用含n的代数式表示).
如图,已知A1,A2,A3,…,An,An+1是x轴上的点,且OA1=A1A2=A2A3=…=AnAn+1=1,分别过点A1,A2,A3,…,An,An+1作x轴的垂线交直线y=$\frac{1}{2}$x于点B1,B2,B3,…,Bn,Bn+1,连接A1B2,B1A2,A2B3,B2A3,…,AnBn+1,BnAn+1,依次相交于点P1,P2,P3,…,Pn,△A1B1P1,△A2B2P2,…,△AnBnPn的面积依次记为S1,S2,S3,…,Sn,则Sn=$\frac{{n}^{2}}{8n+4}$(请用含n的代数式表示).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{10}$ | B. | $\sqrt{6}$ | C. | 2.5 | D. | $\frac{20}{7}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com