
【题目】将两张完全相同的矩形纸片![]() 、
、![]() 按如图方式放置,
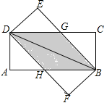
按如图方式放置,![]() 为重合的对角线.重叠部分为四边形
为重合的对角线.重叠部分为四边形![]() ,
,

![]() 试判断四边形
试判断四边形![]() 为何种特殊的四边形,并说明理由;
为何种特殊的四边形,并说明理由;
![]() 若
若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
【答案】(1)四边形![]() 是菱形.(2)
是菱形.(2)![]() .
.
【解析】
(1)由四边形ABCD、FBED是完全相同的矩形,可得出△DAB≌△DEB(SAS),进而可得出∠ABD=∠EBD,根据矩形的性质可得AB∥CD、DF∥BE,即四边形DHBG是平行四边形,再根据平行线的性质结合∠ABD=∠EBD,即可得出∠HDB=∠HBD,由等角对等边可得出DH=BH,由此即可证出DHBG是菱形;
(2)设DH=BH=x,则AH=8-x,在Rt△ADH中,利用勾股定理即可得出关于x的一元一次方程,解之即可得出x的值,再根据菱形的面积公式即可求出菱形DHBG的面积.
解:![]() 四边形
四边形![]() 是菱形.理由如下:
是菱形.理由如下:
∵四边形![]() 、
、![]() 是完全相同的矩形,
是完全相同的矩形,
∴![]() ,
,![]() ,
,![]() .
.
在![]() 和
和![]() 中,
中,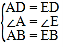 ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴四边形![]() 是平行四边形,
是平行四边形,![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() 是菱形.
是菱形.
![]() 由
由![]() ,设
,设![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,即
,即![]() ,
,
解得:![]() ,即
,即![]() ,
,
∴菱形![]() 的面积为
的面积为![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】仙降是瑞安重要的制鞋基地,其生产的鞋子畅销世界各地,某制鞋企业欲将![]() 件产品运往
件产品运往![]() 三地销售,运往
三地销售,运往![]() 地的费用为18元/件,运往
地的费用为18元/件,运往![]() 地的费用为20元/件,运往
地的费用为20元/件,运往![]() 地的费用为17元/件,要求运往
地的费用为17元/件,要求运往![]() 地的件数与运往
地的件数与运往![]() 地的件数相同. 设安排
地的件数相同. 设安排![]() 件产品运往
件产品运往![]() 地.
地.
(1)若![]() ①运往
①运往![]() 地件数为 件(用含
地件数为 件(用含![]() 的代数式表示);②若总运费不超过1850元,则运往
的代数式表示);②若总运费不超过1850元,则运往![]() 地至少有多少件?
地至少有多少件?
(2)若总运费为1900元,则![]() 的最大值为 .(直接写出答案)
的最大值为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)请画出△ABC关于直线m(直线m上各点的横坐标都为1)对称的图形.(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C′三点的坐标.
(3)平面内任一点P(x,y)关于直线m对称点的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B两地相距20千米,甲、乙两人都从A地去B地,图中l1和l2分别表示甲、乙两人所走路程s(千米)与时间t(小时)之间的关系,下列说法:①乙晚出发1小时;②乙出发3小时后追上甲;③甲的速度是4千米/时;④乙先到达B地.其中正确的是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
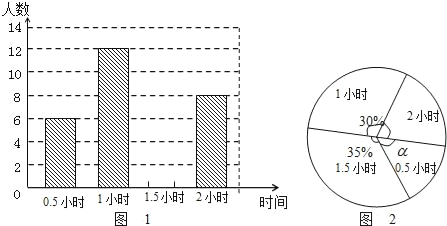
【题目】为了贯彻“减负增效”精神,掌握九年级600名学生每天的自主学习情况,某校学生会随机抽查了九年级的部分学生,并调查他们每天自主学习的时间.根据调查结果,制作了两幅不完整的统计图(图1,图2),请根据统计图中的信息回答下列问题:
(1)本次调查的学生人数是 人;
(2)图2中α是 度,并将图1条形统计图补充完整;
(3)请估算该校九年级学生自主学习时间不少于1.5小时有 人;
(4)老师想从学习效果较好的4位同学(分别记为A、B、C、D,其中A为小亮)随机选择两位进行学习经验交流,用列表法或树状图的方法求出选中小亮A的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象在第一
的图象在第一

象限相交于点![]() ,过点
,过点![]() 分别作
分别作![]() 轴、
轴、![]() 轴的垂线,垂足为点
轴的垂线,垂足为点![]() 、
、![]() ,如果四边形
,如果四边形![]() 是正方形.
是正方形.
![]() 求一次函数的解析式.
求一次函数的解析式.
![]() 一次函数的图象与
一次函数的图象与![]() 轴交于点
轴交于点![]() .在
.在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使得
,使得![]() 最小?若存在,请求出
最小?若存在,请求出![]() 点坐标及最小值;若不存在,请说明理由.
点坐标及最小值;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com