
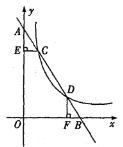
【题目】如图,在平面直角坐标系中,直线AB与y轴和x轴分别交于点A、点B,与反比例函数y=![]() 在第一象限的图像交于点C(1,6)、点D(3,n).过点C作CE⊥y轴于E,过点D作DF⊥x轴于F.
在第一象限的图像交于点C(1,6)、点D(3,n).过点C作CE⊥y轴于E,过点D作DF⊥x轴于F.
(1)求m、n的值;
(2)求直线AB的函数解析式;
(3)试证明:△AEC≌△DFB;
【答案】(1)m=6,n=2;(2)y=-2x+8;(3)见解析
【解析】
(1)将点C(1,6)代入y=![]() 求出m的值,再根据函数解析式求出n的值;
求出m的值,再根据函数解析式求出n的值;
(2)根据C、D的坐标,利用待定系数法求出一次函数解析式;
(3)再根据直线的解析式求得A,B的坐标,从而求得线段AE,CE,DF,BF的长,根据SAS即可证明两个三角形全等.
(1)将C(1,6)代入,m=1×6=6,则函数解析式为y=![]() ,
,
将D(3,n)代入y=![]() 得,n=
得,n=![]() =2,
=2,
故m=6,n=2.
(2)设AB的解析式为y=kx+b,
将C(1,6)、D(3,2)分别代入解析式得,
![]() ,解得
,解得![]() ,
,
则函数解析式为y=2x+8;
(3)证明:∵y=2x+8
令x=0,y=8,y=2x+8=0,解得x=4
∴A(0,8),B (4,0)
∵CE⊥y轴,DF⊥x轴,
∴∠AEC=∠DFB=90![]()
∵AE=DF=86=2,CE=BF=43=1,
则△AEC≌△DFB.


科目:初中数学 来源: 题型:
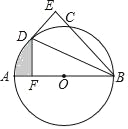
【题目】如图,AB为⊙O的直径,C为⊙O上一点,∠ABC的平分线交⊙O于点D,DE⊥BC于点E.
(1)试判断DE与⊙O的位置关系,并说明理由;
(2)过点D作DF⊥AB于点F,若BE=3![]() ,DF=3,求图中阴影部分的面积.
,DF=3,求图中阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△AOB中,∠O=90°,AO=8cm,BO=6cm,点C从A点出发,在边AO上以4cm/s的速度向O点运动,与此同时,点D从点B出发,在边BO上以3cm/s的速度向O点运动,过OC的中点E作CD的垂线EF,则当点C运动了________s时,以C点为圆心,2cm为半径的圆与直线EF相切.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于某一函数给出如下定义:若存在实数![]() ,当其自变量的值为
,当其自变量的值为![]() 时,其函数值等于
时,其函数值等于![]() ,则称
,则称![]() 为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差
为这个函数的不变值.在函数存在不变值时,该函数的最大不变值与最小不变值之差![]() 称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度
称为这个函数的不变长度.特别地,当函数只有一个不变值时,其不变长度![]() 为零.例如,图1中的函数有0,1两个不变值,其不变长度
为零.例如,图1中的函数有0,1两个不变值,其不变长度![]() 等于1.
等于1.
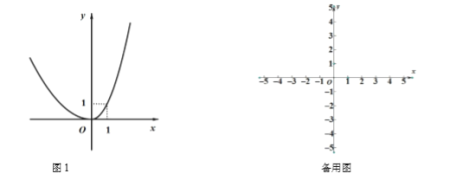
(1)分别判断函数![]() ,
,![]() 有没有不变值?如果有,请写出其不变长度;
有没有不变值?如果有,请写出其不变长度;
(2)函数![]() 且
且![]() ,求其不变长度
,求其不变长度![]() 的取值范围;
的取值范围;
(3)记函数![]() 的图像为
的图像为![]() ,将
,将![]() 沿
沿![]() 翻折后得到的函数图像记为
翻折后得到的函数图像记为![]() ,函数
,函数![]() 的图像由
的图像由![]() 和
和![]() 两部分组成,若其不变长度
两部分组成,若其不变长度![]() 满足
满足![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
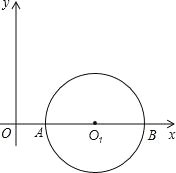
【题目】已知:半径为1的⊙O1与x轴交于A、B两点,圆心O1的坐标为(2,0),二次函数y=﹣x2+bx+c的图象经过A、B两点,其顶点为F.
(1)求b、c的值及二次函数顶点F的坐标;
(2)写出将二次函数y=﹣x2+bx+c的图象向下平移1个单位再向左平移2个单位的图象的函数表达式;
(3)经过原点O的直线l与⊙O相切,求直线l的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某店只销售某种进价为40元/kg的产品,已知该店按60元kg出售时,每天可售出100kg,后来经过市场调查发现,单价每降低1元,则每天的销售量可增加10kg.
(1)若单价降低2元,则每天的销售量是_____千克,每天的利润为_____元;若单价降低x元,则每天的销售量是_____千克,每天的利润为______元;(用含x的代数式表示)
(2)若该店销售这种产品计划每天获利2240元,单价应降价多少元?
(3)当单价降低多少元时,该店每天的利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
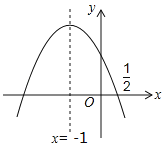
【题目】(4分)如图,抛物线![]() 的对称轴是
的对称轴是![]() .且过点(
.且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com