
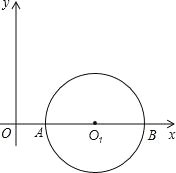
����Ŀ����֪���뾶Ϊ1�ġ�O1��x�ύ��A��B���㣬Բ��O1������Ϊ��2��0�������κ���y=��x2+bx+c��ͼ��A��B���㣬�䶥��ΪF��
��1����b��c��ֵ�����κ�������F�����ꣻ
��2��д�������κ���y=��x2+bx+c��ͼ������ƽ��1����λ������ƽ��2����λ��ͼ��ĺ�������ʽ��
��3������ԭ��O��ֱ��l���O���У���ֱ��l�ĺ�������ʽ��
���𰸡���1��b=4 �� c=-3��F��2��1�� ��2��y=��![]() ��3��y=��
��3��y=��![]() x
x
��������
��1�����ݡ�O1�İ뾶��Բ�ĵ����꣬�����A��B��������꣬Ȼ�����Ǵ��������ߵĽ���ʽ�У������b��c��ֵ�������ɸ��ݶ��κ����Ľ���ʽ�������F�����꣮
��2����ԭ�����ߵĽ���ʽ��Ϊ����ʽ��Ȼ���ٰ���Ŀ�����IJ��裬һ��һ���Ľ���ƽ�ƣ�
��3����ԭ���ֱ����������������ֻ�����ֱ����Բ���е�����꣬����ȷ��ֱ��l�Ľ���ʽ��������Բ�ĶԳ��Կ�֪������������ֱ��lӦ����������
�⣺��1������֪�ã�A��1��0����B��3��0��
�����⣺![]()
��ã�![]()
��y=��x2+4x��3=����x��2��2+1
�ඥ��F��2��1��
��2��y=��x2
��3���辭��ԭ��O��ֱ��l��y=kx��k��0�����O1�����ڵ�C
��O1C��OC��OO1=2��O1C=1
��OC=![]() ����O1OC=30��
����O1OC=30��
���C��������xc��yc��
��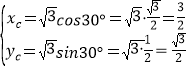
��![]()
![]() k����k=
k����k=![]()
��y=![]() x
x
��Բ�ĶԳ��ԣ���һ��ֱ��l�Ľ���ʽ��y=��![]() x��
x��


 ��ѧȫ��������ѵ��ϵ�д�
��ѧȫ��������ѵ��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
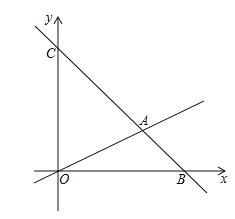
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�����![]() ��ֱ��
��ֱ��![]() ��ֱ��
��ֱ��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ������
������![]() ���߶�
���߶�![]() ������
������![]() ���˶�.
���˶�.
��1����ֱ��![]() �ĺ�����ϵʽ.
�ĺ�����ϵʽ.
��2����![]() �����.
�����.
��3���Ƿ���ڵ�![]() ��ʹ
��ʹ![]() �������
�������![]() �������ȣ������������ʱ��
�������ȣ������������ʱ��![]() �����ꣻ�������ڣ�˵������.
�����ꣻ�������ڣ�˵������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
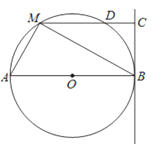
����Ŀ����ͼ��ֱ��BC��뾶Ϊ6�ġ�O�����ڵ�B����M��Բ�ϵĶ��㣬����M��MC��BC������ΪC��MC���O���ڵ�D��ABΪ��O��ֱ��������MA��MB����MC�ij�Ϊx����6��x��12����
��1����x=9ʱ����BM�ij��͡�ABM�������
��2���Ƿ���ڵ�M��ʹMDDC=20�������ڣ������x��ֵ���������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������ABCD�У�AB=12����EΪBC���е㣬��CDΪֱ������ԲCFD����FΪ��Բ���е㣬����AF��EF��ͼ����Ӱ���ֵ�����ǣ�������
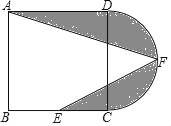
A. 18+36�� B. 24+18�� C. 18+18�� D. 12+18��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ij����С��Ϊ�˲���ɽBC�ĸ߶ȣ��ڵ���A�����ɽ��B������45����Ȼ�������¶�Ϊi=1��![]() ������AD����200�״ﵽD������ʱ��D�����ɽ��B������Ϊ60������ɽ��BC������������ţ���
������AD����200�״ﵽD������ʱ��D�����ɽ��B������Ϊ60������ɽ��BC������������ţ���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��AB��y���x��ֱ��ڵ�A����B���뷴��������y��![]() �ڵ�һ����ͼ���ڵ�C(1��6)����D(3��n)������C��CE��y����E������D��DF��x����F��
�ڵ�һ����ͼ���ڵ�C(1��6)����D(3��n)������C��CE��y����E������D��DF��x����F��
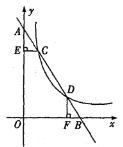
��1����m��n��ֵ��
��2����ֱ��AB�ĺ�������ʽ��
��3����֤������AEC�ա�DFB��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���߳�Ϊ1��������ABCD����AC ��DB���ڵ�H��DEƽ����ADB����AC�ڵ�E������BE���ӳ�������AD�ڵ�F��
��1����֤��DC=EC��
��2�����EAF�������

![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��y��x+b��˫����y��![]() ���ڵ�A����1����5�������ֱ���x�ᡢy�ύ�ڵ�C��B��
���ڵ�A����1����5�������ֱ���x�ᡢy�ύ�ڵ�C��B��
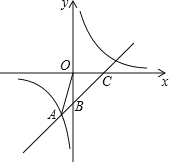
��1��ֱ��д��b���� ����m���� ����
��2������ͼ��ֱ��д������ʽx+b��![]() �Ľ⼯Ϊ�� ����
�Ľ⼯Ϊ�� ����
��3������D��x����������ϣ��Ƿ�����Ե�D��C��B���ɵ����������OAB���ƣ������ڣ������D�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() ��
��![]() ƽ��
ƽ��![]() ��
��
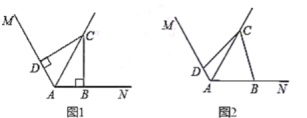
��1����ͼ1��![]() ����
����![]() ����֤��
����֤��![]() ��
��
��2����ͼ2��![]() ����
����![]() ����1���еĽ����Ƿ���Ȼ�������������������֤����������������˵�����ɣ�
����1���еĽ����Ƿ���Ȼ�������������������֤����������������˵�����ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com