
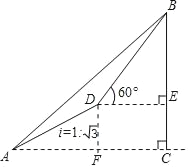
【题目】如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为i=1:![]() 的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,求山高BC(结果保留根号).
的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,求山高BC(结果保留根号).

【答案】BC= 100+100![]() (米).
(米).
【解析】
作DF⊥AC于F,根据i=1:![]() ,AD=200米,可知tan∠DAF=
,AD=200米,可知tan∠DAF=![]() ,可知∠DAF=30°,进而求出DF的长度,根据所给角的度数可知△ABD是等腰三角形,AD=BD,解直角三角形BDE可求出BE,根据BC=BE+CE求出BC即可.
,可知∠DAF=30°,进而求出DF的长度,根据所给角的度数可知△ABD是等腰三角形,AD=BD,解直角三角形BDE可求出BE,根据BC=BE+CE求出BC即可.
作DF⊥AC于F.
∵DF:AF=1:![]() ,AD=200米,
,AD=200米,
∴tan∠DAF=![]() ,
,
∴∠DAF=30°,
∴DF=![]() AD=
AD=![]() ×200=100(米),
×200=100(米),
∵∠DEC=∠BCA=∠DFC=90°,
∴四边形DECF是矩形,
∴EC=DF=100(米),
∵∠BAC=45°,BC⊥AC,
∴∠ABC=45°,
∵∠BDE=60°,DE⊥BC,
∴∠DBE=90°﹣∠BDE=90°﹣60°=30°,
∴∠ABD=∠ABC﹣∠DBE=45°﹣30°=15°,∠BAD=∠BAC﹣∠1=45°﹣30°=15°,
∴∠ABD=∠BAD,
∴AD=BD=200(米),
在Rt△BDE中,sin∠BDE=![]() ,
,
∴BE=BDsin∠BDE=200×![]() =100
=100![]() (米),
(米),
∴BC=BE+EC=100+100![]() (米).
(米).


科目:初中数学 来源: 题型:
【题目】我国古代数学的许多发现都曾位居世界前列,其中“杨辉三角”(如图所示)就是一例.

这个三角形的构造法则为:两腰上的数都是1,其余每个数均为其上方左右两数之和.事实上,这个三角形给出了![]() (
(![]() 为正整数)的展开式(按
为正整数)的展开式(按![]() 的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1、
的次数由大到小的顺序排列)的系数规律.例如,在三角形中第三行的三个数1、![]() 、1,恰好对应
、1,恰好对应![]() 展开式中各项的系数;第四行的四个数1、
展开式中各项的系数;第四行的四个数1、![]() 、
、![]() 、1,恰好对应着
、1,恰好对应着![]() 展开式中各项的系数等等.根据上面的规律,
展开式中各项的系数等等.根据上面的规律,![]() 的展开式中各项系数最大的数为_______;式子
的展开式中各项系数最大的数为_______;式子![]()
![]() 的值为______.
的值为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角三角形ABC中,∠ACB=90°,∠B=36°,D是AB的中点,ED⊥AB交BC于E,连接CD,则∠CDE:∠ECD=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,且满足
,且满足![]() .
.

(1)![]() 于
于![]() ,交
,交![]() 轴于
轴于![]() ,求
,求![]() 点坐标;
点坐标;
(2)过点![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)![]() 为第一象限一点,
为第一象限一点,![]() 交
交![]() 轴于
轴于![]() .在
.在![]() 上截取
上截取![]() ,
,![]() 为
为![]() 的中点,求
的中点,求![]() 的度数.
的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】列方程解应用题:
(1)一个箱子,如果装橙子可以装18个,如果装梨可以装16个,现共有橙子、梨400个,而且装梨的箱子是装橙子箱子的2倍.请算一下,装橙子和装梨的箱子各多少个?
(2)一群小孩分一堆苹果,每人3个多7个,每人4个少3个,求有几个小孩?几个苹果?
(3)一架飞机在两城之间飞行,风速为24千米/时.顺风飞行需要2小时50分,逆风飞行需要3小时,求无风时飞机的速度和两城之间的航程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:三角形ABC中,∠A=90,AB=AC,D为BC的中点,如图,E,F分别是AB,AC上的点,且BE=AF,求证:△DEF为等腰直角三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,点D是等边△ABC的边BC上一点,连接AD,以AD为一边,向右作等边三角形ADE,连接CE,求证:AC=CD+CE.
(类比探究)
(1)如果点D在BC的延长线上,其它条件不变,请在图②的基础上画出满足条件的图形,写出线段AC,CD,CE之间的数量关系,并说明理由.
(2)如果点D在CB的延长线上,请在图③的基础上画出满足条件的图形,并直接写出AC,CD,CE之间的数量关系,不需要说明理由.数量关系:_______.



查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知E是平行四边形ABCD中BC边的中点,连接AE并延长AE交DC的延长线于点F。
(1)求证:△ABE≌△FCE;
(2)连接AC、BF,若AE=![]() BC,求证:四边形ABFC为矩形;
BC,求证:四边形ABFC为矩形;
(3)在(2)条件下,当△ABC再满足一个什么条件时,四边形ABFC为正方形。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com