
【题目】如图①,点D是等边△ABC的边BC上一点,连接AD,以AD为一边,向右作等边三角形ADE,连接CE,求证:AC=CD+CE.
(类比探究)
(1)如果点D在BC的延长线上,其它条件不变,请在图②的基础上画出满足条件的图形,写出线段AC,CD,CE之间的数量关系,并说明理由.
(2)如果点D在CB的延长线上,请在图③的基础上画出满足条件的图形,并直接写出AC,CD,CE之间的数量关系,不需要说明理由.数量关系:_______.



【答案】证明见解析;类比探究:(1)CE﹣CD=AC;(2)AC=CD﹣CE.
【解析】
先证明△ABD≌△ACE,得出BD=CE,即可证出CE+CD=BD+CD=BC=AC;
类比探究:
(1)先证明△ABD≌△ACE,得出BD=CE,即可证出CE-CD=BD-CD=BC=AC;
(2)先证明△ABD≌△ACE,得出BD=CE,即可得出数量关系:AC=CD-CE.
∵△ABC和△ADE均为等边三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
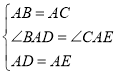 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CE+CD=BD+CD=BC=AC;
类比探究:( 1)CE﹣CD=AC;
如图②:

∵△ABC和△ADE均为等边三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
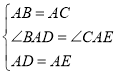 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CE﹣CD=BD﹣CD=BC=AC.
( 2)数量关系:AC=CD﹣CE.
如图③:
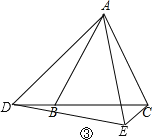
∵△ABC和△ADE均为等边三角形,
∴AB=AC=BC,AD=AE,∠BAC=∠DAE=60°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
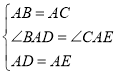 ,
,
∴△ABD≌△ACE(SAS),
∴BD=CE,
∴CD﹣CE=CD﹣BD=BC=AC.
故答案为:AC=CD﹣CE.


科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A.一个游戏中奖的概率是![]() ,则做100次这样的游戏一定会中奖
,则做100次这样的游戏一定会中奖
B.为了了解全国中学生的心理健康状况,应采用普查的方式
C.一组数据0,1,2,1,1的众数和中位数都是1
D.若甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为i=1:![]() 的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,求山高BC(结果保留根号).
的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,求山高BC(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() ,
,![]() 相交于
相交于![]() 点,将直线
点,将直线![]() 绕点
绕点![]() 顺时针旋转,分别交
顺时针旋转,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,下列说法不正确的是( )
,下列说法不正确的是( )

A. 当![]() 时,四边形
时,四边形![]() 一定为平行四边形
一定为平行四边形
B. 当四边形![]() 为直角梯形时,线段
为直角梯形时,线段![]()
C. 当![]() 时,四边形
时,四边形![]() 一定为菱形
一定为菱形
D. 在旋转的过程中,线段![]() 与
与![]() 总相等
总相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC中,AB=AC,∠BAC=90°,点D是平面内一点;

(1)如图1, BD⊥CD,∠DCA=30°,则∠BAD=
(2)如图2,若∠BDC=45°,点F是CD中点,求证:AF⊥CD;
(3)如图3,∠BDA=3∠CBD,BD=![]() ,求△BCD的面积.
,求△BCD的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
科目:初中数学 来源: 题型:
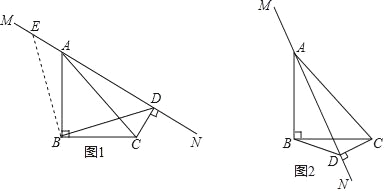
【题目】如图1,在Rt△ABC中,∠ABC=90°,BA=BC,直线MN是过点A的直线CD⊥MN于点D,连接BD.
(1)观察猜想张老师在课堂上提出问题:线段DC,AD,BD之间有什么数量关系.经过观察思考,小明出一种思路:如图1,过点B作BE⊥BD,交MN于点E,进而得出:DC+AD= BD.
(2)探究证明
将直线MN绕点A顺时针旋转到图2的位置写出此时线段DC,AD,BD之间的数量关系,并证明
(3)拓展延伸
在直线MN绕点A旋转的过程中,当△ABD面积取得最大值时,若CD长为1,请直接写BD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com