Question

【题目】如图，中，，，，对角线，相交于点，将直线绕点顺时针旋转，分别交，于点，，下列说法不正确的是（ ）

A. 当时，四边形一定为平行四边形

B. 当四边形为直角梯形时，线段

C. 当时，四边形一定为菱形

D. 在旋转的过程中，线段与总相等

Answer 1

【答案】B

【解析】

根据平行四边形的判定得出AB∥EF，AD∥BC，即可得出四边形ABEF一定为平行四边形；利用直角三角形的面积求出AB×AC=AM×BC，求出EF即可；当∠AOF=45°时，

可得到△BAO是等腰直角三角形，从而得到EF⊥BD．再由OF=OE，根据对角线互相垂直平分的四边形是菱形知，四边形BEDF一定为菱形；通过证明△AEO≌△CEO，可得到AF=EC．

A．当∠AOF=90°时．

∵ABCD中，AB⊥AC，∴AB∥EF．

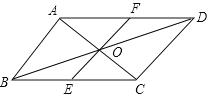
∵AD∥BC，∴四边形ABEF一定为平行四边形．故选项A正确；

B．作AM⊥BC，当四边形ABEF为直角梯形时，∴EF⊥BC，∴AM=EF．

∵AB⊥AC，AB=1，BC=，∴AC=2，∴AB×AC=AM×BC，∴1×2=AM×，∴AM=．

故选项B错误．

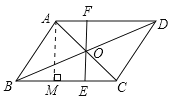
C．当∠AOF=45°时．

∵AB⊥AC，AB=1，BC=，∴AC==2．

∵OA=OC=AC=1，∴△BAO是等腰直角三角形，∴∠AOB=45°．

∵∠AOF=45°，∴∠BOF=90°，∴EF⊥BD．

∵△AOF≌△CEO，∴OF=OE，根据对角线互相垂直平分的四边形是菱形知，四边形BEDF一定为菱形，故C正确；

D．∵AF∥BE，∴∠FAO=∠OCE．

∵AO=CO，∠AOF=∠COE，∴△AEO≌△CEO，∴AF=EC，故D正确．

故选B．