
【题目】如图,三角形ABC是边长为6的等边三角形,P是AC边上任意一点(与A、C两点不重合).Q是CB延长线上一点,且始终满足条件BQ=AP,过P作PE⊥AB于E,连接PQ交AB于D.
(1)如图(1)当∠CQP=30°时.求AP的长.
(2)如图(2),当P在任意位置时,求证:DE=![]() AB.
AB.

【答案】(1)2;(2)证明见解析.
【解析】
试题分析:(1)作PF∥BC交AB于点F.根据等边三角形的性质及直角三角形的性质就可以求出∠QPC=∠DPA=90°,得出AB=3AP而求出结论;
(2)作PF∥BC交AB于点F.根据等边三角形的性质就可以得出△PFD≌△QBD就有DF=DB,由等腰三角形的性质就可以得出AE=EF,由EF+FD=ED就可以得出结论.
试题解析:(1)如图(1),作PF∥BC交AB于点F,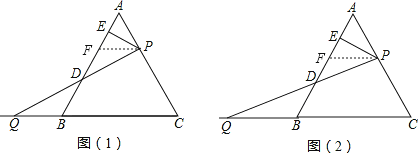
∴∠AFP=∠ABC,∠APF=∠C.∠PFD=∠QBD,∠FPD=∠BQD.
∵△ABC是等边三角形,
∴∠A=∠ABC=∠C=60°.AB=BC=AC.
∴∠AFP=60°,∠APF=60°,
∴∠AFP=∠APF=∠A=60°,
∴△AFP是等边三角形,
∴AF=AP=PF.
∵PE⊥AB,
∴AE=EF.
∵∠CQP=30°,∠C=60°,
∴∠QPC=90°,
∴∠DPA=90°,
∴∠ADP=30°.
∴AD=2AP.
∴AD=2AF.
∵DF+AF=AD,
∴DF+AF=2AF,
∴DF=AF,
∵BQ=AP,
∴BQ=FP.
在△PFD和△QBD中
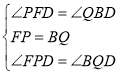 ,
,
∴△PFD≌△QBD(ASA),
∴FD=BD.
∴BD=DF=AF=![]() AB.
AB.
∵AB=6,
∴AF=2,
∴AP=2.
答:AP的长为2;
(2)如图2,作PF∥BC交AB于点F.
∴∠AFP=∠ABC,∠APF=∠C.∠PFD=∠QBD,∠FPD=∠BQD.
∵△ABC是等边三角形,
∴∠A=∠ABC=∠C=60°.AB=BC=AC.
∴∠AFP=60°,∠APF=60°,
∴∠AFP=∠APF=∠C=60°,
∴△AFP是等边三角形,
∴AF=AP=PF.
∵PE⊥AB,
∴AE=EF=![]() AF.
AF.
∵BQ=AP,
∴BQ=FP.
由(1)知,△PFD≌△QBD(ASA),
∴FD=BD=![]() BF.
BF.
∵ED=EF+DF=![]() AF+
AF+![]() BF,
BF,
∴ED=![]() (AF+BF),
(AF+BF),
∴ED=![]() AB.
AB.


科目:初中数学 来源: 题型:
【题目】张庄甲、乙两家草莓采摘园的草莓销售价格相同,“春节期间”,两家采摘园将推出优惠方案,甲园的优惠方案是:游客进园需购买门票,采摘的草莓六折优惠;乙园的优惠方案是:游客进园不需购买门票,采摘园的草莓超过一定数量后,超过部分打折优惠.优惠期间,某游客的草莓采摘量为![]() (千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与
(千克),在甲园所需总费用为y甲(元),在乙园所需总费用为y乙(元),y甲、y乙与![]() 之间的函数关系如图所示,折线OAB表示y乙与
之间的函数关系如图所示,折线OAB表示y乙与![]() 之间的函数关系.
之间的函数关系.
(1)甲采摘园的门票是 元,在乙园采摘草莓超过______![]() 后超过部分有打折优惠;
后超过部分有打折优惠;
(2)当采摘量![]() 时,采摘多少千克草莓,甲、乙两家采摘园的总费用相同.
时,采摘多少千克草莓,甲、乙两家采摘园的总费用相同.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABP与![]() 是两个全等的等边三角形,且
是两个全等的等边三角形,且![]() ,有下列四个结论:①
,有下列四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④四边形ABCD是轴对称图形,其中正确的有
,④四边形ABCD是轴对称图形,其中正确的有

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于![]() 的一元二次方程
的一元二次方程![]() .下列论断:
.下列论断:![]() 若
若![]() ,则它有一根为
,则它有一根为![]() ;
;![]() 若它有一根为
若它有一根为![]() ,则一定有
,则一定有![]() ;
;![]() 若
若![]() ,则它一定有两个不相等的实数根;其中正确的是( )
,则它一定有两个不相等的实数根;其中正确的是( )
A. ![]() 个 B.
个 B. ![]() 个 C.
个 C. ![]() 个 D.
个 D. ![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知一次函数y=![]() x-3与反比例函数y=
x-3与反比例函数y=![]() 的图象相交于点A(4,n),与x轴相交于点B.以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,则点D的坐标为_________.
的图象相交于点A(4,n),与x轴相交于点B.以AB为边作菱形ABCD,使点C在x轴正半轴上,点D在第一象限,则点D的坐标为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:∠BAC的平分线与BC的垂直平分线相交于点D,DE⊥AB,DF⊥AC,垂足分别为E,F,AB=6,AC=4,则BE=_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A.一个游戏中奖的概率是![]() ,则做100次这样的游戏一定会中奖
,则做100次这样的游戏一定会中奖
B.为了了解全国中学生的心理健康状况,应采用普查的方式
C.一组数据0,1,2,1,1的众数和中位数都是1
D.若甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
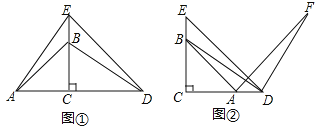
【题目】已知△ABC与△DEC是两个大小不同的等腰直角三角形.
(1)如图①所示,连接AE,DB,试判断线段AE和DB的数量和位置关系,并说明理由;
(2)如图②所示,连接DB,将线段DB绕D点顺时针旋转90°到DF,连接AF,试判断线段DE和AF的数量和位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() ,
,![]() 相交于
相交于![]() 点,将直线
点,将直线![]() 绕点
绕点![]() 顺时针旋转,分别交
顺时针旋转,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,下列说法不正确的是( )
,下列说法不正确的是( )

A. 当![]() 时,四边形
时,四边形![]() 一定为平行四边形
一定为平行四边形
B. 当四边形![]() 为直角梯形时,线段
为直角梯形时,线段![]()
C. 当![]() 时,四边形
时,四边形![]() 一定为菱形
一定为菱形
D. 在旋转的过程中,线段![]() 与
与![]() 总相等
总相等
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com