
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,且满足
,且满足![]() .
.

(1)![]() 于
于![]() ,交
,交![]() 轴于
轴于![]() ,求
,求![]() 点坐标;
点坐标;
(2)过点![]() 作
作![]() 于
于![]() ,交
,交![]() 于
于![]() ,若
,若![]() ,求
,求![]() 的长;
的长;
(3)![]() 为第一象限一点,
为第一象限一点,![]() 交
交![]() 轴于
轴于![]() .在
.在![]() 上截取
上截取![]() ,
,![]() 为
为![]() 的中点,求
的中点,求![]() 的度数.
的度数.
【答案】(1)M(0,2);(2)AN=4;(3)∠OPF=45°.
【解析】
(1)先由条件推出△AOC是等腰直角三角形,再推出△BOM是等腰直角三角形,根据OB=2,得出OM=2,即可得出M的坐标;
(2)由等角的余角相等可得∠BCO=∠OAN=30°,再判定△BOC≌△NOA(ASA),得到BC=NA,再根据Rt△BOC中,BC=2BO=4,即可得AN=4;
(3)连接OF,把△OCF绕点O顺时针旋转90°至△OAD处,连接DP,由旋转可得,AD=CF=EF,∠OCF=∠OAD,OF=OD,再判定△PEF≌△PAD,得出PF=PD,∠FPE=∠DPA,进而判定△OPF≌△OPD,即可出结果.
(1)由题可得,ac≥0,ca≥0,
∴a=c,即OA=OC,
∴△AOC是等腰直角三角形,
∴∠OAD=45,
又∵BD⊥AC,
∴∠ABD=45,
又∵∠BOM=90,
∴△BOM是等腰直角三角形,
∴OB=OM,
∵![]() ,且a=c,
,且a=c,
∴b=2,即OB=2,
∴OM=2,
∴M(0,2);
(2)∵∠CAN=15°,∠OAC=45°,
∴∠OAN=30°,
∵AG⊥BC,CO⊥AO,
∴∠CNG+∠BCO=90°,∠ANO+∠OAN=90°,
∵∠ANO=∠CNG,
∴∠BCO=∠OAN=30°,
在△BOC和△NOA中,
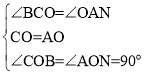
∴△BOC≌△NOA(ASA),
∴BC=NA,
又∵Rt△BOC中,∠BCO=30°,
∴BC=2BO=4,
∴AN=4;
(3)如图3,连接OF,把△OCF绕点O顺时针旋转90°至△OAD处,连接DP,
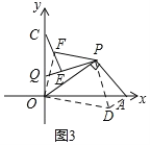
由旋转可得,AD=CF=EF,∠OCF=∠OAD,OF=OD,
∵∠AOQ+∠APQ=180°,
∴∠OAP+∠OQP=180°,
又∵∠EQC+∠OQP=180°,
∴∠OAP=∠EQC,
∴∠PEF=∠PAD,
在△PEF和△PAD中,
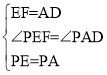
∴△PEF≌△PAD(SAS),
∴PF=PD,∠FPE=∠DPA,
∴∠FPD=∠QPA=90°,
∵在△OPF和△OPD中,
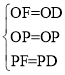
∴△OPF≌△OPD(SSS),
∴∠OPF=∠OPD=![]() ∠FPD=45°.
∠FPD=45°.


科目:初中数学 来源: 题型:
【题目】如图,△ABP与![]() 是两个全等的等边三角形,且
是两个全等的等边三角形,且![]() ,有下列四个结论:①
,有下列四个结论:①![]() ,②
,②![]() ,③
,③![]() ,④四边形ABCD是轴对称图形,其中正确的有
,④四边形ABCD是轴对称图形,其中正确的有

A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是
A.一个游戏中奖的概率是![]() ,则做100次这样的游戏一定会中奖
,则做100次这样的游戏一定会中奖
B.为了了解全国中学生的心理健康状况,应采用普查的方式
C.一组数据0,1,2,1,1的众数和中位数都是1
D.若甲组数据的方差![]() ,乙组数据的方差
,乙组数据的方差![]() ,则乙组数据比甲组数据稳定
,则乙组数据比甲组数据稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
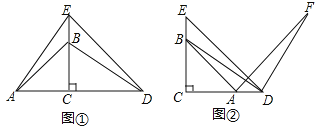
【题目】已知△ABC与△DEC是两个大小不同的等腰直角三角形.
(1)如图①所示,连接AE,DB,试判断线段AE和DB的数量和位置关系,并说明理由;
(2)如图②所示,连接DB,将线段DB绕D点顺时针旋转90°到DF,连接AF,试判断线段DE和AF的数量和位置关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在等腰三角形ABC中,∠ABC=90度,D是AC边上的动点,连结BD,E、F分别是AB、BC上的点,且DE⊥DF.、(1)如图1,若D为AC边上的中点.
(1)填空:∠C= ,∠DBC= ;
(2)求证:△BDE≌△CDF.
(3)如图2,D从点C出发,点E在PD上,以每秒1个单位的速度向终点A运动,过点B作BP∥AC,且PB=AC=4,点E在PD上,设点D运动的时间为t秒(0≤1≤4)在点D运动的过程中,图中能否出现全等三角形?若能,请直接写出t的值以及所对应的全等三角形的对数,若不能,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育老师为了解本校九年级女生1分钟“仰卧起坐”体育测试项目的达标情况,从该校九年级136名女生中,随机抽取了20名女生,进行了1分钟仰卧起坐测试,获得数据如下:
收集数据:抽取20名女生的1分钟仰卧起坐测试成绩(个)如下:
38 46 42 52 55 43 59 46 25 38
35 45 51 48 57 49 47 53 58 49
(1)整理、描述数据:请你按如下分组整理、描述样本数据,把下列表格补充完整:
范围 | 25≤x≤29 | 30≤x≤34 | 35≤x≤39 | 40≤x≤44 | 45≤x≤49 | 50≤x≤54 | 55≤x≤59 |
人数 |
|
|
|
|
|
|
|
(说明:每分钟仰卧起坐个数达到49个及以上时在中考体育测试中可以得到满分)
(2)分析数据:样本数据的平均数、中位数、满分率如下表所示:
平均数 | 中位数 | 满分率 |
46.8 | 47.5 | 45% |
得出结论:①估计该校九年级女生在中考体育测试中1分钟“仰卧起坐”项目可以得到满分的人数为 ;
②该中心所在区县的九年级女生的1分钟“仰卧起坐”总体测试成绩如下:
平均数 | 中位数 | 满分率 |
45.3 | 49 | 51.2% |
请你结合该校样本测试成绩和该区县总体测试成绩,为该校九年级女生的1分钟“仰卧起坐”达标情况做一下评估,并提出相应建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某测量小组为了测量山BC的高度,在地面A处测得山顶B的仰角45°,然后沿着坡度为i=1:![]() 的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,求山高BC(结果保留根号).
的坡面AD走了200米达到D处,此时在D处测得山顶B的仰角为60°,求山高BC(结果保留根号).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 中,
中,![]() ,
,![]() ,
,![]() ,对角线
,对角线![]() ,
,![]() 相交于
相交于![]() 点,将直线
点,将直线![]() 绕点
绕点![]() 顺时针旋转,分别交
顺时针旋转,分别交![]() ,
,![]() 于点
于点![]() ,
,![]() ,下列说法不正确的是( )
,下列说法不正确的是( )

A. 当![]() 时,四边形
时,四边形![]() 一定为平行四边形
一定为平行四边形
B. 当四边形![]() 为直角梯形时,线段
为直角梯形时,线段![]()
C. 当![]() 时,四边形
时,四边形![]() 一定为菱形
一定为菱形
D. 在旋转的过程中,线段![]() 与
与![]() 总相等
总相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是某同学对多项式(x2-4x+2)(x2-4x+6)+4进行因式分解的过程.
解:设x2-4x=y
原式=(y+2)(y+6)+4 (第一步)
= y2+8y+16 (第二步)
=(y+4)2 (第三步)
=(x2-4x+4)2 (第四步)
回答下列问题:
(1)该同学第二步到第三步运用了因式分解的_______.
A.提取公因式 B.平方差公式 C.两数和的完全平方公式 D.两数差的完全平方公式
(2)该同学因式分解的结果是否彻底?________.(填“彻底”或“不彻底”)
若不彻底,请直接写出因式分解的最后结果_________.
(3)请你模仿以上方法尝试对多项式(x2-2x)(x2-2x+2)+1进行因式分解.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com