
【题目】已知![]() ,
,![]() 平分
平分![]() .
.
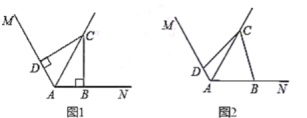
(1)在图1中![]() ,若
,若![]() ,求证:
,求证:![]() ;
;
(2)在图2中![]() ,若
,若![]() ,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由.
【答案】(1)见解析;(2)成立,见解析
【解析】
(1)根据含30°角的直角三角形的性质进行证明;
(2)作CE⊥AM、CF⊥AN于E、F.根据角平分线的性质,得CE=CF,根据等角的补角相等,得∠CDE=∠ABC,再根据AAS得到△CDE≌△CBF,则DE=BF.再由∠MAN=120°,AC平分∠MAN,得到∠ECA=∠FCA=30°,从而根据30°所对的直角边等于斜边的一半,得到AE=![]() AC,AF=
AC,AF=![]() AC,等量代换后即可证明AD+AB=AC仍成立.
AC,等量代换后即可证明AD+AB=AC仍成立.
(1)证明:∵∠MAN=120°,AC平分∠MAN,
∴∠CAD=∠CAB=60°.
又∠ABC=∠ADC=90°,
∴AD=![]() AC,AB=
AC,AB=![]() AC,
AC,
∴AB+AD=AC;
(2)解:结论仍成立.
理由如下:
作CE⊥AM、CF⊥AN于E、F.
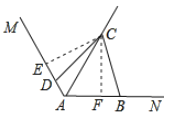
则∠CED=∠CFB=90°,
∵AC平分∠MAN,
∴CE=CF.
∵∠ABC+∠ADC=180°,∠ADC+∠CDE=180°
∴∠CDE=∠ABC,
在△CDE和△CBF中,
 ,
,
∴△CDE≌△CBF(AAS),
∴DE=BF.
∵∠MAN=120°,AC平分∠MAN,
∴∠MAC=∠NAC=60°,
∴∠ECA=∠FCA=30°,
在Rt△ACE与Rt△ACF中,
则有AE=![]() AC,AF=
AC,AF=![]() AC,
AC,
则AD+AB
=AD+AF+BF
=AD+AF+DE
=AE+AF
=![]() AC+
AC+![]() AC
AC
=AC.
∴AD+AB=AC.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
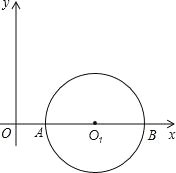
【题目】已知:半径为1的⊙O1与x轴交于A、B两点,圆心O1的坐标为(2,0),二次函数y=﹣x2+bx+c的图象经过A、B两点,其顶点为F.
(1)求b、c的值及二次函数顶点F的坐标;
(2)写出将二次函数y=﹣x2+bx+c的图象向下平移1个单位再向左平移2个单位的图象的函数表达式;
(3)经过原点O的直线l与⊙O相切,求直线l的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
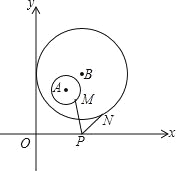
【题目】如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,以1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=x+4的图象与二次函数y=ax(x﹣2)的图象相交于A(﹣1,b)和B,点P是线段AB上的动点(不与A、B重合),过点P作PC⊥x轴,与二次函数y=ax(x﹣2)的图象交于点C.

(1)求a、b的值
(2)求线段PC长的最大值;
(3)若△PAC为直角三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用无刻度的直尺按要求作图,请保留画图痕迹,不需要写作法。
(1)在8×6的正方形网格中,请用无刻度直尺画一个![]() 与
与![]() 面积相等,顶点在格点上 .(画出一个满足条件即可)
面积相等,顶点在格点上 .(画出一个满足条件即可)
(2)在8×6的正方形网格中,请用无刻度直尺画一个与![]() 面积相等,且以
面积相等,且以![]() 为边的平行四边形,顶点在格点上.(画出一个满足条件即可)
为边的平行四边形,顶点在格点上.(画出一个满足条件即可)


查看答案和解析>>
科目:初中数学 来源: 题型:
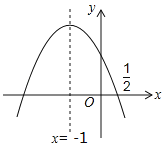
【题目】(4分)如图,抛物线![]() 的对称轴是
的对称轴是![]() .且过点(
.且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
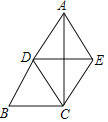
【题目】已知:如图,在△ABC中,∠ACB=90°,点D是斜边AB的中点,DE∥BC,且CE=CD.
(1)求证:∠B=∠DEC;
(2)求证:四边形ADCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
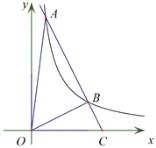
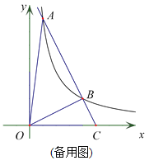
【题目】如图,在平面直角坐标系 xOy中,直线ykxb与 x轴相交于点A,与反比例函数在第一象限内的图像相交于点 A(1,8)、B(m,2).
(1)求该反比例函数和直线y kxb的表达式;
(2)求证:ΔOBC为直角三角形;
(3)设∠ACO=α,点Q为反比例函数在第一象限内的图像上一动点,且满足90°-α<∠QOC<α,求点Q的横坐标q的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在ABCD中,E是CD延长线上的一点,BE与AD交于点F,DE=![]() CD.
CD.
(1)求证:△ABF∽△CEB;
(2)若△DEF的面积为2,求ABCD的面积.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com