
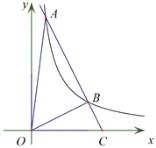
【题目】如图,在平面直角坐标系 xOy中,直线ykxb与 x轴相交于点A,与反比例函数在第一象限内的图像相交于点 A(1,8)、B(m,2).
(1)求该反比例函数和直线y kxb的表达式;
(2)求证:ΔOBC为直角三角形;
(3)设∠ACO=α,点Q为反比例函数在第一象限内的图像上一动点,且满足90°-α<∠QOC<α,求点Q的横坐标q的取值范围.
【答案】(1)![]() ;
;![]() ;(2)证明见解析;(3)
;(2)证明见解析;(3)![]() .
.
【解析】
(1)首先利用待定系数法求得反比例函数的解析式,然后求得B的坐标,则利用待定系数法即可求得直线的解析式;
(2)过点B作BD⊥OC于点D,在直角△OBD和直角△OBC中,利用勾股定理求得![]() 和
和![]() ,然后利用勾股定理的逆定理即可证明;
,然后利用勾股定理的逆定理即可证明;
(3)分成Q在B的左侧和右侧两种情况讨论,当在右侧时一定不成立,当在左侧时,判断是否存在点Q时∠QCO=90°-α即可.
(1)设反比例函数的解析式是y=kx,

把(1,8)代入得k=8,
则反比例函数表达式为![]() ,
,
把(m,2)代入得![]() ,
,
则B的坐标是(4,2).
根据题意得:![]() ,
,
解得:![]() ,
,
,则直线表达式y=2x+10;
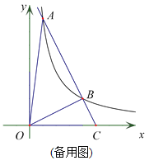
(2)过点B作BD⊥OC于点D,(图1)则D的坐标是(4,0).
在y=2x+10中,令y=0,解得x=5,则OC=5.
∵在直角△OBD中,BD=2,DC=OCOD=54=1,
则![]() ,
,
同理,直角△BCD中, ![]() ,
,
∴![]() ,
,
∴△OBC是直角三角形;
(3)当Q在B的右侧时一定不成立,
在y=2x+10中,令x=0,则y=10,

则当Q在的左边时,(图2)tan∠ACO=tanα=2,
则tan(90°α)= ![]() .
.
当∠QCO=90°α时,Q的横坐标是p,则纵坐标是![]() ,
,
tan∠QCO=tan(90°α)= ![]() :(5p)=
:(5p)= ![]()
即![]() ,
,
△=254×16=39<0,则Q不存在,
故当Q在AB之间时,满足条件,
因而2<q<4.


科目:初中数学 来源: 题型:
【题目】直线y=x+b与双曲线y=![]() 交于点A(﹣1,﹣5).并分别与x轴、y轴交于点C、B.
交于点A(﹣1,﹣5).并分别与x轴、y轴交于点C、B.
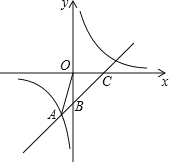
(1)直接写出b= ,m= ;
(2)根据图象直接写出不等式x+b<![]() 的解集为 ;
的解集为 ;
(3)若点D在x轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在,请求出D的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
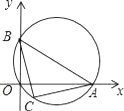
【题目】如图,点A,B分别在x轴、y轴上(OA>OB),以AB为直径的圆经过原点O,C是![]() 的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有( )
的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有( )
A. 3个 B. 2个 C. 1个 D. 0个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在半径为27m的广场中央,点O的上空安装了一个照明光源S,S射向地面的光束呈圆锥形,其轴截面SAB的顶角为120°(如图),求光源离地面的垂直高度SO.(精确到0.1m;![]() =1.44,
=1.44,![]() =1.732,
=1.732,![]() =2.236,以上数据供参考)
=2.236,以上数据供参考)

查看答案和解析>>
科目:初中数学 来源: 题型:
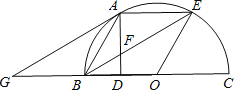
【题目】如图,点A,E是半圆周上的三等分点,直径BC=2,AD⊥BC,垂足为D,连接BE交AD于F,过A作AG∥BE交BC于G.
(1)判断直线AG与⊙O的位置关系,并说明理由.
(2)求线段AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,BD=![]() BC,等边△BEF的顶点F在BC上,边EF交AD于点P,若BE=10,BC=14,则PE的长为( )
BC,等边△BEF的顶点F在BC上,边EF交AD于点P,若BE=10,BC=14,则PE的长为( )

A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,分别以直角△ABC的斜边AB,直角边AC为边向△ABC外作等边△ABD和等边△ACE,F为AB的中点,DE与AB交于点G,EF与AC交于点H,∠ACB=90°,∠BAC=30°.给出如下结论:
①EF⊥AC;②四边形ADFE为菱形;③AD=4AG;④FH=![]() BD
BD
其中正确结论的为______(请将所有正确的序号都填上).

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com