
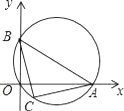
【题目】如图,点A,B分别在x轴、y轴上(OA>OB),以AB为直径的圆经过原点O,C是![]() 的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有( )
的中点,连结AC,BC.下列结论:①AC=BC;②若OA=4,OB=2,则△ABC的面积等于5;③若OA﹣OB=4,则点C的坐标是(2,﹣2).其中正确的结论有( )
A. 3个 B. 2个 C. 1个 D. 0个
【答案】A
【解析】
①∵AB为直径,
∴∠ACB=900,
∴①正确;
②∵C是![]() 的中点,
的中点,
∴![]() =
=![]() ,
,
∴AC=BC,
∴②正确;
③在Rt△AOB中,OA=4,OB=2,
∴AB=![]() =
=![]() ,
,
在Rt△ABC中,AC=BC=![]() AB=
AB=![]() ,
,
∴△ABC的面积=![]() ×AC×BC=
×AC×BC=![]() ×
×![]() ×
×![]() =5,
=5,
∴③正确;
④如图,
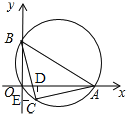
过点C作CD⊥OA,DE⊥OB,
∴∠BEC=∠ADC=90°
在△BCE和△ACD中,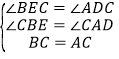 ,
,
∴△BCE≌△ACD,
∴AD=BE,CE=CD,
∵∠DOE=∠OEC=∠ODC=90°,
∴四边形ODCE是矩形,
∵CE=CD,
∴矩形ODCE是正方形,
∴OD=OD=CD=CE,
∵AD=OAOD,BE=OB+BE=OB+OD,
∵AD=BE
∴OAOD=OB+OD,
∵OAOB=4,
∴OD=2,
∴CD=CE=2,
∴C(2,2)
∴④正确,
故选:A.


科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=x+4的图象与二次函数y=ax(x﹣2)的图象相交于A(﹣1,b)和B,点P是线段AB上的动点(不与A、B重合),过点P作PC⊥x轴,与二次函数y=ax(x﹣2)的图象交于点C.

(1)求a、b的值
(2)求线段PC长的最大值;
(3)若△PAC为直角三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
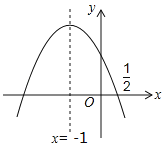
【题目】(4分)如图,抛物线![]() 的对称轴是
的对称轴是![]() .且过点(
.且过点(![]() ,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
,0),有下列结论:①abc>0;②a﹣2b+4c=0;③25a﹣10b+4c=0;④3b+2c>0;⑤a﹣b≥m(am﹣b);其中所有正确的结论是 .(填写正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
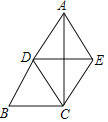
【题目】已知:如图,在△ABC中,∠ACB=90°,点D是斜边AB的中点,DE∥BC,且CE=CD.
(1)求证:∠B=∠DEC;
(2)求证:四边形ADCE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
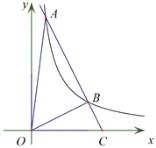
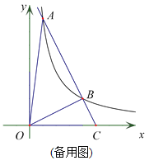
【题目】如图,在平面直角坐标系 xOy中,直线ykxb与 x轴相交于点A,与反比例函数在第一象限内的图像相交于点 A(1,8)、B(m,2).
(1)求该反比例函数和直线y kxb的表达式;
(2)求证:ΔOBC为直角三角形;
(3)设∠ACO=α,点Q为反比例函数在第一象限内的图像上一动点,且满足90°-α<∠QOC<α,求点Q的横坐标q的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读与计算:请阅读以下材料,并完成相应的任务.
斐波那契(约1170﹣1250)是意大利数学家,他研究了一列数,这列数非常奇妙,被称为斐波那契数列(按照一定顺序排列着的一列数称为数列).后来人们在研究它的过程中,发现了许多意想不到的结果,在实际生活中,很多花朵(如梅花、飞燕草、万寿菊等)的瓣数恰是斐波那契数列中的数.斐波那契数列还有很多有趣的性质,在实际生活中也有广泛的应用.斐波那契数列中的第n个数可以用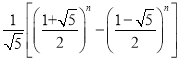 表示(其中,n≥1).这是用无理数表示有理数的一个范例.
表示(其中,n≥1).这是用无理数表示有理数的一个范例.

任务:请根据以上材料,通过计算求出斐波那契数列中的第1个数和第2个数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com