
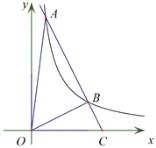
【题目】直线y=x+b与双曲线y=![]() 交于点A(﹣1,﹣5).并分别与x轴、y轴交于点C、B.
交于点A(﹣1,﹣5).并分别与x轴、y轴交于点C、B.
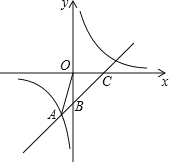
(1)直接写出b= ,m= ;
(2)根据图象直接写出不等式x+b<![]() 的解集为 ;
的解集为 ;
(3)若点D在x轴的正半轴上,是否存在以点D、C、B构成的三角形与△OAB相似?若存在,请求出D的坐标;若不存在,请说明理由.
【答案】(1)-4,5;(2) x<﹣1或0<x<5;(3)存在,D的坐标是(6,0)或(20,0).
【解析】
(1)把A的坐标分别代入一次函数与反比例函数的解析式,即可求得b和m的值;
(2)根据图象即可直接写出,即反比例函数的图象在一次函数的图象上部的部分x的取值;
(3)求得△OAB的边长,点D在x轴的正半轴上,可以分D在线段OC上(不在O点)或线段OC的延长线上两种情况讨论,依据相似三角形的对应边的比相等即可求得.
解:(1)把A(﹣1,﹣5)代入y=x+b得:﹣5=﹣1+b,解得:b=﹣4.
把A(﹣1,﹣5)代入y=![]() ,得:m=(﹣1)(﹣5)=5.
,得:m=(﹣1)(﹣5)=5.
故答案是:﹣4,5;
(2)解集为:x<﹣1或0<x<5,
故答案是:x<﹣1或0<x<5;
(3)OA=![]() =
=![]() ,
,
在y=x﹣4中,令x=0,解得y=﹣4,则B的坐标是(0,﹣4).
令y=0,解得:x=4,则C的坐标是(4,0).
故OB=4,AB=![]() =
=![]() ,BC=4
,BC=4![]() ,OC=4.
,OC=4.
∴OB=OC,即△OBC是等腰直角三角形,
∴∠OCB=∠OBC=45°,∠BCE=135°.
过A作AF⊥y轴于点F.则△ABF是等腰直角△,∠ABF=45°,∠ABO=135°.
1)当D在线段OC(不与O重合)上时,两个三角形一定不能相似;
2)当D在线段OC的延长线上时,设D的坐标是(x,0),则CD=x﹣4,
∠ABO=∠BCD=135°,
当△AOB∽△DBC时,![]() =
=![]() ,即
,即![]() =
=![]() ,
,
解得:x=6,
则D的坐标是(6,0);
当△AOB∽△BDC时,![]() ,即
,即![]() =
=![]() ,
,
解得:x=20,
则D的坐标是(20,0).
则D的坐标是(6,0)或(20,0).


 发散思维新课堂系列答案
发散思维新课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在矩形OABC中,点O为原点,点A的坐标为(0,8),点C的坐标为(6,0).抛物线y=﹣![]() x2+bx+c经过点A、C,与AB交于点D.
x2+bx+c经过点A、C,与AB交于点D.
(1)求抛物线的函数解析式;
(2)点P为线段BC上一个动点(不与点C重合),点Q为线段AC上一个动点,AQ=CP,连接PQ,设CP=m,△CPQ的面积为S.
①求S关于m的函数表达式;
②当S最大时,在抛物线y=﹣![]() x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.
x2+bx+c的对称轴l上,若存在点F,使△DFQ为直角三角形,请直接写出所有符合条件的点F的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
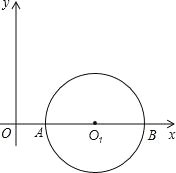
【题目】已知:半径为1的⊙O1与x轴交于A、B两点,圆心O1的坐标为(2,0),二次函数y=﹣x2+bx+c的图象经过A、B两点,其顶点为F.
(1)求b、c的值及二次函数顶点F的坐标;
(2)写出将二次函数y=﹣x2+bx+c的图象向下平移1个单位再向左平移2个单位的图象的函数表达式;
(3)经过原点O的直线l与⊙O相切,求直线l的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某中学举行“中国梦校园好声音”歌手大赛,高、初中部根据初赛成绩,各选出5名选手组成初中代表队和高中代表队参加学校决赛.两个队各选出的5名选手的决赛成绩如图所示.

(1)根据图示填写下表;
平均数(分) | 中位数(分) | 众数(分) | |
初中部 | 85 | ||
高中部 | 85 | 100 |
(2)结合两队成绩的平均数和中位数,分析哪个队的决赛成绩较好;
(3)计算两队决赛成绩的方差并判断哪一个代表队选手成绩较为稳定.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个布口袋里装着白、红、黑三种颜色的小球,它们除颜色之外没有任何其它区别,其中有白球3只、红球2只、黑球1只.袋中的球已经搅匀.
(1)闭上眼睛随机地从袋中取出1只球,求取出的球是黑球的概率;
(2)若取出的第1只球是红球,将它放在桌上,闭上眼睛从袋中余下的球中再随机地取出1只球,这时取出的球还是红球的概率是多少?
(3)若取出一只球,将它放回袋中,闭上眼睛从袋中再随机地取出1只球,两次取出的球都是白球概率是多少?(用列表法或树状图法计算)
查看答案和解析>>
科目:初中数学 来源: 题型:
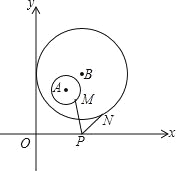
【题目】如图,平面直角坐标系中,分别以点A(2,3)、点B(3,4)为圆心,以1、3为半径作⊙A、⊙B,M,N分别是⊙A、⊙B上的动点,P为x轴上的动点,则PM+PN的最小值为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知一次函数y=x+4的图象与二次函数y=ax(x﹣2)的图象相交于A(﹣1,b)和B,点P是线段AB上的动点(不与A、B重合),过点P作PC⊥x轴,与二次函数y=ax(x﹣2)的图象交于点C.

(1)求a、b的值
(2)求线段PC长的最大值;
(3)若△PAC为直角三角形,请直接写出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系 xOy中,直线ykxb与 x轴相交于点A,与反比例函数在第一象限内的图像相交于点 A(1,8)、B(m,2).
(1)求该反比例函数和直线y kxb的表达式;
(2)求证:ΔOBC为直角三角形;
(3)设∠ACO=α,点Q为反比例函数在第一象限内的图像上一动点,且满足90°-α<∠QOC<α,求点Q的横坐标q的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com