
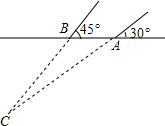
 如图,在修建某条地铁时,科技人员利用探测仪在地面A、B两个探测点探测到地下C处有金属回声.已知A、B两点相距8米,探测线AC,BC与地面的夹角分别是30°和45°,试确定有金属回声的点C的深度是多少米?
如图,在修建某条地铁时,科技人员利用探测仪在地面A、B两个探测点探测到地下C处有金属回声.已知A、B两点相距8米,探测线AC,BC与地面的夹角分别是30°和45°,试确定有金属回声的点C的深度是多少米?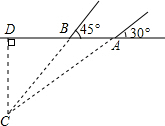 解:如图,作CD⊥AB于点D.
解:如图,作CD⊥AB于点D.| 3 |
| 3 |
| 3 |
| 3 |


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
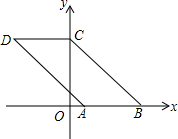 如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )
如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )| A、14 | B、16 | C、18 | D、20 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、x0<5 |
| B、1<x0<5 |
| C、-3≤x0<1 |
| D、x0<1 |
查看答案和解析>>
科目:初中数学 来源: 题型:
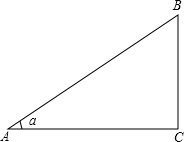 如图:为了测楼房BC的高,在距离楼房10米的A处,测得楼顶B的仰角为,那么楼房BC的高为( )
如图:为了测楼房BC的高,在距离楼房10米的A处,测得楼顶B的仰角为,那么楼房BC的高为( )| A、10tana(米) | ||||||
B、
| ||||||
| C、10sina(米) | ||||||
D、
|
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com