
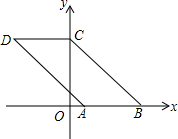
 如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )
如图,已知点A(1,0),B(4,0),将线段AB平移得到线段CD,点B的对应点C恰好落在y轴上,且四边形ABCD的面积为9,则四边形ABCD的周长为( )| A、14 | B、16 | C、18 | D、20 |
| OB2+OC2 |
| 42+32 |


科目:初中数学 来源: 题型:
| k |
| 3 |
| A、y1<y2 |
| B、y1=y2 |
| C、y1>y2 |
| D、不能比较 |
查看答案和解析>>
科目:初中数学 来源: 题型:
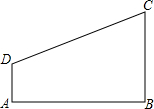 已知,如图,四边形ABCD,∠A=∠B=Rt∠
已知,如图,四边形ABCD,∠A=∠B=Rt∠| 5 |
查看答案和解析>>
科目:初中数学 来源: 题型:
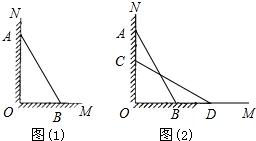 如图(1),一架长为20米云梯AB斜靠在竖直的墙ON上,这时云梯下端B到墙底端O的距离BO=12米,在下列结论中,正确的是( )
如图(1),一架长为20米云梯AB斜靠在竖直的墙ON上,这时云梯下端B到墙底端O的距离BO=12米,在下列结论中,正确的是( )A、当消防员爬到距离地面
| ||
| B、如图(2),当梯子顶端A沿墙下滑3米时,底端B向外移动3米 | ||
| C、如图(2),在梯子下滑过程中,梯子AB与墙ON,地面OM构成的三角形面积存在最大值,最大值为100米2 | ||
D、若在射线ON上存在一点G,使得△ABG为等腰三角形,则AG=
|
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、P为∠A,∠B两角平分线的交点 |
| B、P为AC,AB两边的垂直平分线的交点 |
| C、P为AC,AB两边上的高的交点 |
| D、P为∠A的平分线与边BC的垂直平分线的交点 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、a<m<n<b |
| B、a<m<b<n |
| C、m<a<b<n |
| D、m<a<n<b |
查看答案和解析>>
科目:初中数学 来源: 题型:
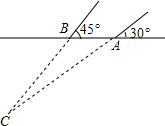 如图,在修建某条地铁时,科技人员利用探测仪在地面A、B两个探测点探测到地下C处有金属回声.已知A、B两点相距8米,探测线AC,BC与地面的夹角分别是30°和45°,试确定有金属回声的点C的深度是多少米?
如图,在修建某条地铁时,科技人员利用探测仪在地面A、B两个探测点探测到地下C处有金属回声.已知A、B两点相距8米,探测线AC,BC与地面的夹角分别是30°和45°,试确定有金属回声的点C的深度是多少米?查看答案和解析>>
科目:初中数学 来源: 题型:
 在一条笔直的道路上有相距9千米的A,B两地,甲以3km/h的速度从A地走向B地,出发0.5h后,乙从B地以4.5km/h的速度走向A地,甲、乙两人走到各自终点停止.设甲行走的时间为t(h).
在一条笔直的道路上有相距9千米的A,B两地,甲以3km/h的速度从A地走向B地,出发0.5h后,乙从B地以4.5km/h的速度走向A地,甲、乙两人走到各自终点停止.设甲行走的时间为t(h).查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com