
【题目】在长方形纸片ABCD中,AB=m,AD=n,将两张边长分别为6和4的正方形纸片按图1,图2两种方式放置(图1,图2中两张正方形纸片均有部分重叠),长方形中未被这两张正方形纸片覆盖的部分用阴影表示,设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2.
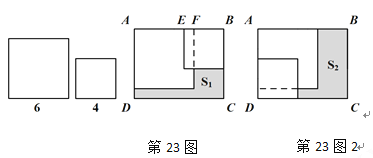
(1)在图1中,EF= ,BF= ;(用含m的式子表示)
(2)请用含m、n的式子表示图1,图2中的s1,s2,若m-n=2,请问S2-S1的值为多少?
【答案】(1)EF=10-m, BF= m-6;(2)8.
【解析】
(1)根据AF+BE-EF=AB可表示出EF的长,根据BF=BE-EF可表示出BF的长;
(2)先利用割补法分别表示出S1和S2的值,再相减,然后把m-n=2代入化简后的结果计算即可.
(1)∵AF+BE-EF=AB,
∴6+4-EF=m,
∴EF=10-m,
∴BF=BE-EF=4-(10-m)=m-6;
(2)∵S1=6(n-6)+(m-6)(n-4)=mn-4m-12,
S2=6(m-6)+(m-4)(n-6)=mn-4n-12,
∴S2-S1=( mn-4n-12)-( mn-4m-12)=4m-4n=4(m-n).
∵m-n=2,
∴S2-S1=4(m-n)=8.


科目:初中数学 来源: 题型:
【题目】如图,点O是直线AB上的一点,∠COD是直角,OE平分∠BOC.
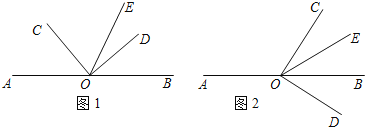
(1)如图(1),若∠AOC=![]() ,求∠DOE的度数;
,求∠DOE的度数;
(2)如图(2),将∠COD绕顶点O旋转,且保持射线OC在直线AB上方,在整个旋转过程中,当∠AOC的度数是多少时,∠COE=2∠DOB.
查看答案和解析>>
科目:初中数学 来源: 题型:
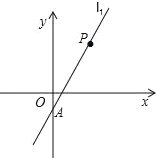
【题目】如图,已知直线l1经过点A(0,﹣1)与点P(2,3),另一条直线l2经过点P,且与y轴交于点B(0,m).
(1)求直线l1的解析式;
(2)若△APB的面积为3,求m的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(3,0),∠ABO=30°,且AB⊥BC.
(1)求直线BC和AB的解析式;
(2)将点B沿某条直线折叠到点O,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;
(3)在平面直角坐标系内是否存在两个点,使得这两个点与B、C两点构成的四边形是正方形?若存在,请求出这两点的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八个边长为1的正方形如图摆放在平面直角坐标系中,经过原点的一条直线l将这八个正方形分成面积相等的两部分,则该直线l的解析式为( )

A.y=﹣x B.y=﹣![]() x C.y=﹣
x C.y=﹣![]() x D.y=﹣
x D.y=﹣![]() x
x
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC沿BC边上的中线AD平移到△A'B'C'的位置,已知△ABC的面积为9,阴影部分三角形的面积为4.若AA'=1,则A'D等于( )

A. 2 B. 3 C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在下列选项中,是反比例函数关系的为
A. 在直角三角形中,30°角所对的直角边y与斜边x之间的关系
B. 在等腰三角形中,顶角y与底角x之间的关系
C. 圆的面积S与它的直径d之间的关系
D. 面积为20的菱形,其中一条对角线y与另一条对角线x之间的关系
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两超市(大型商场)同时开业,为了吸引顾客,都举行有奖酬宾活动:凡购物满100元,均可得到一次摸奖的机会.在一个纸盒里装有2个红球和2个白球,除颜色外其它都相同,摸奖者一次从中摸出两个球,根据球的颜色决定送礼金券(在他们超市使用时,与人民币等值)的多少.(如下表) 甲超市:
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 5 | 10 | 5 |
乙超市:
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 10 | 5 | 10 |
(1)用树状图表示得到一次摸奖机会时中礼金券的所有情况;
(2)如果只考虑中奖因素,你将会选择去哪个超市购物?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com