练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

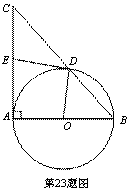
        如图，在△ABC中，∠CAB=90°，∠CBA=50°，以AB为直径作⊙O交BC于点D，点E在边AC上，且满足ED=EA.（1）求∠DOA的度数；   （2）求证：直线ED与⊙O相切.

     



    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


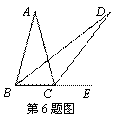
    如图,在△ABC中，AB  =   AC，∠A   =   30°，E为BC延长线上一点，

    ∠ABC与∠ACE的平分线相交于点D，则∠D的度数为

    A. 15°          B. 17.5°            C. 20°     D. 22.5°

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    甲乙两人制作某种机械零件。已知甲每小时比乙多做3个，甲做96个所用时间与乙做84个所用时间相等，求甲乙两人每小时各做多少个零件？

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一组数据的众数是                 .

     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    计算           

    查看答案和解析>>

    科目：初中数学 来源： 题型：


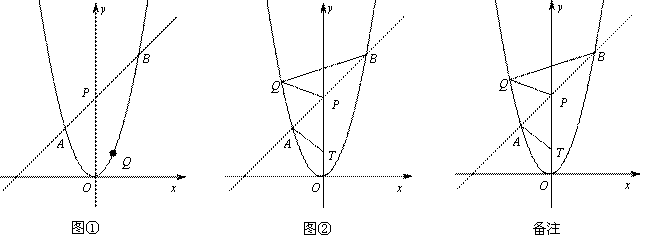
       如图，在平面直角坐标系xOy中，将抛物线的对称轴绕着点P（，2）顺时针旋转45°后与该抛物线交于A、B两点，点Q是该抛物线上的一点.

      （1）求直线AB的函数表达式；

      （2）如图①，若点Q在直线AB的下方，求点Q到直线AB的距离的最大值；

      （3）如图②，若点Q在y轴左侧，且点T（0，t）（t<2）是直线PO上一点，当以P、B、Q为顶点的三角形与△PAT相似时，求所有满足条件的t的值.

     


     

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    数学课上，老师让学生尺规作图画Rt△ABC，使其斜边AB=c，一条直角边BC=a．小明的作法如图所示，你认为这种作法中判断∠ACB是直角的依据是（　　）

    　

    A．

    勾股定理

    　

    B．

    直径所对的圆心角是直角

    　

    C．

    勾股定理的逆定理

    　

    D．

    90°的圆周角所对的弦是直径

    　

      

    查看答案和解析>>

    科目：初中数学 来源： 题型：


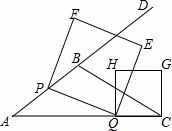
    如图，在△ABC中，AB=5，AC=9，S△ABC=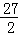，动点P从A点出发，沿射线AB方向以每秒5个单位的速度运动，动点Q从C点出发，以相同的速度在线段AC上由C向A运动，当Q点运动到A点时，P、Q两点同时停止运动，以PQ为边作正方形PQEF（P、Q、E、F按逆时针排序），以CQ为边在AC上方作正方形QCGH．

    （1）求tanA的值；

    （2）设点P运动时间为t，正方形PQEF的面积为S，请探究S是否存在最小值？若存在，求出这个最小值，若不存在，请说明理由；

    （3）当t为何值时，正方形PQEF的某个顶点（Q点除外）落在正方形QCGH的边上，请直接写出t的值．

    　

    　  

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    先化简，再求值：其中．

    查看答案和解析>>

    同步练习册答案