
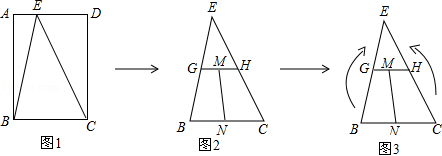
分析 (1)首先确定剪拼之后的四边形是个平行四边形,根据三角形中位线性质定理即可证明;
(2)由三角形中位线的性质可以得出BC=6为定值,进而就有四边形的周长取决于MN的大小,在矩形中探究MN的不同位置关系,当点E在点A或点D时就可以得出MN的最大值,由平行线间垂线段最短就可以得到最小值,从而问题解决
解答 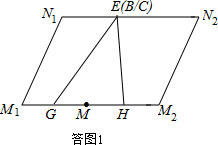 解:(1)画出第三步剪拼之后的四边形M1N1N2M2的示意图,如答图1所示.
解:(1)画出第三步剪拼之后的四边形M1N1N2M2的示意图,如答图1所示.
图中,N1N2=EN1+EN2=NB+NC=BC,
M1M2=M1G+GM+MH+M2H=2(GM+MH)=2GH=BC(三角形中位线定理),
又∵M1M2∥N1N2,
∴四边形M1N1N2M2是一个平行四边形,
故答案为:平行四边形.
(2)如图2所示,是剪拼之前的完整示意图.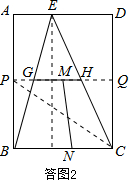 过G、H点作BC边的平行线,分别交AB、CD于P点、Q点,则四边形PBCQ是一个矩形,这个矩形是矩形ABCD的一半.
过G、H点作BC边的平行线,分别交AB、CD于P点、Q点,则四边形PBCQ是一个矩形,这个矩形是矩形ABCD的一半.
∵M是线段GH上的任意一点,N是线段BC上的任意一点,
根据垂线段最短,得到MN的最小值为PQ与BC平行线之间的距离,即MN最小值为4;
而当E点在A点或D点时,MN的最大值等于矩形PQCB的对角线的长度,即
PC=$\sqrt{P{B}^{2}+B{C}^{2}}$=$\sqrt{{4}^{2}+{6}^{2}}$=$2\sqrt{13}$.
∴四边形M1N1N2M2周长的最小值为:12+2×4=20;
四边形M1N1N2M2周长的最大值为:12+2×$2\sqrt{13}$=12+$4\sqrt{13}$.
故答案为:20;(12+$4\sqrt{13}$).
点评 此题主要考查了图形的剪拼以及考查了动手操作能力和空间想象能力,确定剪拼之后的图形,并且探究MN的不同位置关系得出四边形周长的最值是解题关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
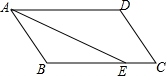 如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )
如图,在平行四边形ABCD中,AD=5,AB=3,AE平分∠BAD交BC边于点E,则线段BE,EC的长度分别为( )| A. | 4和1 | B. | 1和4 | C. | 3和2 | D. | 2和3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
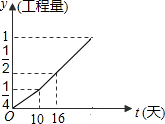 甲、乙两工程队完成某项工程,甲先做了10天,然后乙加入合作,完成剩下的工程.设工程总量为1,若工程进度如下图所示,那么实际完成这项工程所用时间比甲单独完成此项工作所用时间少12天.
甲、乙两工程队完成某项工程,甲先做了10天,然后乙加入合作,完成剩下的工程.设工程总量为1,若工程进度如下图所示,那么实际完成这项工程所用时间比甲单独完成此项工作所用时间少12天.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
| 空气污染指数 | 0~50 | 51~100 | 101~150 | 151~200 | 201~250 | 300以上 |
| 空气质量级别 | 优 | 良 | 轻微污染 | 轻度污染 | 中度污染 | 严重污染 |
| 天 数 | 6 | 12 | 5 | 4 | 2 | 1 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com