
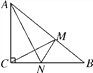
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=6cm,BC=8cm.动点M从点B出发,在BA边上以每秒3cm的速度向定点A运动,同时动点N从点C出发,在CB边上以每秒2cm的速度向点B运动,运动时间为t秒![]() ,连接MN.
,连接MN.
(1)若△BMN与△ABC相似,求t的值;
(2)连接AN,CM,若AN⊥CM,求t的值.
【答案】 (1) △BMN与△ABC相似时,t的值为![]() 或
或![]() ;(2)
;(2) ![]() .
.
【解析】试题分析:(1)、根据Rt△ABC的勾股定理得出AB的长度,然后用含t的代数式分别表示BM、CN和BN的长度,然后根据两种不同的相似得出t的值,得出答案;(2)、过点M作MD⊥CB于点D,从而得出△BDM和△BCA相似,从而求出DM、BD和CD的长度,然后根据垂直得出△CAN和△DCM相似,从而得出t的值.
试题解析:(1)∵∠ACB=90°,AC=6cm,BC=8cm, ∴BA=![]() =10(cm).
=10(cm).
由题意得BM=3tcm,CN=2tcm, ∴BN=(8-2t)cm.
当△BMN∽△BAC时,![]() =
=![]() , ∴
, ∴![]() =
=![]() ,解得t=
,解得t=![]() ;
;
当△BMN∽△BCA时,![]() =
=![]() , ∴
, ∴![]() =
=![]() ,解得t=
,解得t=![]() .
.
综上所述,△BMN与△ABC相似时,t的值为![]() 或
或![]() ;
;
(2)如图,过点M作MD⊥CB于点D,
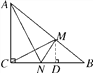
∴∠BDM=∠ACB=90°, 又∵∠B=∠B, ∴△BDM∽△BCA,
∴![]() =
=![]() =
=![]() . ∵AC=6cm,BC=8cm,BA=10cm,BM=3tcm,
. ∵AC=6cm,BC=8cm,BA=10cm,BM=3tcm,
∴DM=![]() tcm,BD=
tcm,BD=![]() tcm, ∴CD=
tcm, ∴CD=![]() cm.
cm.
∵AN⊥CM,∠ACB=90°, ∴∠CAN+∠ACM=90°,∠MCD+∠ACM=90°,
∴∠CAN=∠MCD. ∵MD⊥CB, ∴∠MDC=∠ACB=90°, ∴△CAN∽△DCM,
∴![]() =
=![]() , ∴
, ∴![]() =
=![]() , 解得t=
, 解得t=![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知A(4,n),B(2,4)是一次函数y=kx+b的图象和反比例函数![]() 的图象的两个交点;
的图象的两个交点;

(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)求不等式kx+b![]() <0的解集(请直接写出答案).
<0的解集(请直接写出答案).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是

A.AB∥DC,AD∥BC B.AB=DC,AD=BC
C.AO=CO,BO=DO D.AB∥DC,AD=BC
查看答案和解析>>
科目:初中数学 来源: 题型:
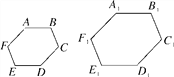
【题目】图中的两个多边形ABCDEF和A1B1C1D1E1F1相似(各字母已按对应关系排列),∠A=∠D1=135°,∠B=∠E1=120°,∠C1=95°.
(1)求∠F的度数;
(2)如果多边形ABCDEF和A1B1C1D1E1F1的相似比是1:1.5,且CD=15cm,求C1D1的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某校数学兴趣小组利用自制的直角三角形硬纸板DEF来测量操场旗杆AB的高度,他们通过调整测量位置,使斜边DF与地面保持平行,并使边DE与旗杆顶点A在同一直线上,已知DE=0.5米,EF=0.25米,目测点D到地面的距离DG=1.5米,到旗杆的水平距离DC=20米,求旗杆的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中∠ABC=90°,,AB=4 cm, BC=3cm,动点P以3cm/s的速度由A向C运动,动点Q同时以1cm/s的速度由B向CB的延长线方向运动,连PQ交AB于D,则当运动时间为____s时,△ADP是以AP为腰的等腰三角形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在第1个![]() 中,
中,![]() ;在边
;在边![]() 上任取一点
上任取一点![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,得到第2个
,得到第2个![]() ;在边
;在边![]() 上任取一点
上任取一点![]() ,延长
,延长![]() 到
到![]() ,使
,使![]() ,得到第3个
,得到第3个![]() …按此做法继续下去,则第
…按此做法继续下去,则第![]() 个三角形中以
个三角形中以![]() 为顶点的底角度数是( )
为顶点的底角度数是( )

A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
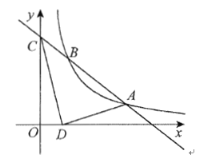
【题目】如图,已知一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于点
的图像交于点![]() 和点
和点![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
(1)反比例函数的表达式 ;一次函数的表达式 .
(2)若在![]() 轴上有一点
轴上有一点![]() ,其横坐标是1,连接
,其横坐标是1,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 分别与正方形
分别与正方形![]() 的顶点
的顶点![]() 、
、![]() 、
、![]() 重合.
重合.
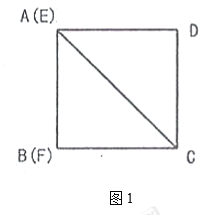
(1)若正方形的边长为![]() ,用含
,用含![]() 的代数式表示:正方形
的代数式表示:正方形![]() 的周长等于_______,
的周长等于_______,![]() 的面积等于_______.
的面积等于_______.
(2)如图2,将![]() 绕点
绕点![]() 顺时针旋转,边
顺时针旋转,边![]() 和正方形的边
和正方形的边![]() 交于点
交于点![]() .连结
.连结![]() ,设旋转角
,设旋转角![]() .
.

①试说明![]() ;
;
②若![]() 有一个内角等于
有一个内角等于![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com