
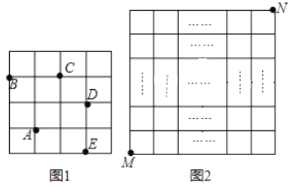
【题目】在每个小正方形的边长为![]() 的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距
的网格图形中,每个小正方形的顶点称为格点.从一个格点移动到与之相距![]() 的另一个格点的运动称为一次跳马变换.例如,在
的另一个格点的运动称为一次跳马变换.例如,在![]() 的正方形网格图形中(如图1),从点
的正方形网格图形中(如图1),从点![]() 经过一次跳马变换可以到达点
经过一次跳马变换可以到达点![]() ,
,![]() ,
,![]() ,
,![]() 等处现有
等处现有![]() 的正方形网格图形(如图2),则从该正方形的顶点
的正方形网格图形(如图2),则从该正方形的顶点![]() 经过跳马变换到达与其相对的顶点
经过跳马变换到达与其相对的顶点![]() ,最少需要跳马变换的次数是( )
,最少需要跳马变换的次数是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案科目:初中数学 来源: 题型:
【题目】如图A、B、C在⊙O上,连接OA、OB、OC,若∠BOC=3∠AOB,劣弧AC的度数是120o,OC=![]() .则图中阴影部分的面积是 ( )
.则图中阴影部分的面积是 ( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线与![]() 轴交于点A,与
轴交于点A,与![]() 轴交点C,抛物线
轴交点C,抛物线![]() 过A,C两点,与x轴交于另一点B.
过A,C两点,与x轴交于另一点B.
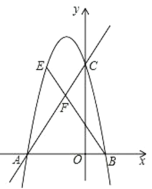
(1)求抛物线的解析式.
(2)在直线AC上方的抛物线上有一动点E,连接BE,与直线AC相交于点F,当![]() 时,求sin∠EBA的值.
时,求sin∠EBA的值.
(3)点N是抛物线对称轴上一点,在(2)的条件下,若点E位于对称轴左侧,在抛物线上是否存在一点M,使以M,N,E,B为顶点的四边形是平行四边形?若存在,直接写出点M的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B为定点,定直线l//AB,P是l上一动点.点M,N分别为PA,PB的中点,对于下列各值:
①线段MN的长;
②△PAB的周长;
③△PMN的面积;
④直线MN,AB之间的距离;
⑤∠APB的大小.
其中会随点P的移动而变化的是( )

A. ②③ B. ②⑤ C. ①③④ D. ④⑤
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xoy中,E(8,0),F(0 , 6).
(1)当G(4,8)时,则∠FGE= °
(2)在图中的网格区域内找一点P,使∠FPE=90°且四边形OEPF被过P点的一条直线分割成两部分后,可以拼成一个正方形.
要求:写出点P点坐标,画出过P点的分割线并指出分割线(不必说明理由,不写画法).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() ,对称轴是直线
,对称轴是直线![]() ,与
,与![]() 轴交于点
轴交于点![]() .若点
.若点![]() ,
,![]() 同时从
同时从![]() 点出发,都以每秒
点出发,都以每秒![]() 个单位长度的速度分别沿
个单位长度的速度分别沿![]() ,
,![]() 边运动.
边运动.
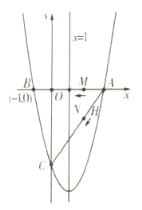
(1)求该二次函数的解析式及点![]() 的坐标,与
的坐标,与![]() 轴的另一个交点
轴的另一个交点![]() 的坐标.
的坐标.
(2)当![]() ,
,![]() 运动到
运动到![]() 秒时,
秒时,![]() 沿
沿![]() 翻折,点
翻折,点![]() 恰好落在
恰好落在![]() 轴上
轴上![]() 点处,请判定此时四边形
点处,请判定此时四边形![]() 的形状,并求出
的形状,并求出![]() 点坐标.
点坐标.
(3)当点![]() 运动到对称轴与
运动到对称轴与![]() 的交点时,点
的交点时,点![]() 往回运动,同时点
往回运动,同时点![]() 则
则![]() 倍的速度继续沿
倍的速度继续沿![]() 运动,在整个运动过程中,以点
运动,在整个运动过程中,以点![]() ,
,![]() ,
,![]() 为顶点的三角形面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
为顶点的三角形面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
(4)在![]() 段的抛物线上有一点
段的抛物线上有一点![]() 到线段
到线段![]() 的距离最大,请求出这个最大距离.
的距离最大,请求出这个最大距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
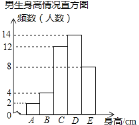
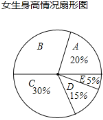
【题目】某校为了了解学生的身高情况,随机对该校男生、女生的身高进行抽样调查,已知抽取的样本中,男生、女生的人数相同,根据所得数据绘制成下面的统计图表:
组别 | A | B | C | D | E |
身高(cm) | x<150 | 150≤x<155 | 155≤x<160 | 160≤x<165 | x≥165 |
根据图表中信息,回答下列问题:
(1)在样本中,男生身高的中位数落在 组(填组别序号),女生身高在B组的人数有 人;
(2)已知该校共有男生500人,女生480人,请估计身高在155≤x<165之间的学生约有多少人?
(3)从男生样本的A、B两组里,随机安排2人参加一项活动,求恰好是1人在A组、1人在B组的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】生物学上研究表明:不同浓度的生长素对植物的生长速度影响不同,在一定范围内,生长素的浓度对植物的生长速度有促进作用,相反,在某些浓度范围,生长速度会变缓慢,甚至阻碍植物生长(阻碍即植物不生长,甚至枯萎).小林同学在了解到这一信息后,决定研究生长素浓度与茶树生长速度的关系,设生长素浓度为x克/升,生长速度为y毫米/天,当x超过4时,茶树的生长速度y与生长素x浓度满足关系式:![]() .实验数据如下表,当生长速度为0时,实验结束.
.实验数据如下表,当生长速度为0时,实验结束.
x | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
y | 2 | 4 | 6 | 8 | 10 | 9 | 7 | 4 | 0 |
(1)如图,建立平面直角坐标系xOy,描出表中各对对应值为坐标的点,画出该函数图象;
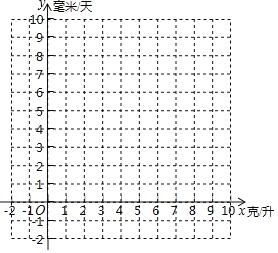
(2)根据上述表格,求出整个实验过程中y与x的函数关系式,并写出自变量x的取值范围;
(3)结合画出的函数图象,写出该函数的一条性质: ;
(4)若直线y=kx+3与上述函数图象有2个交点,则k的取值范围是: .
查看答案和解析>>
科目:初中数学 来源: 题型:
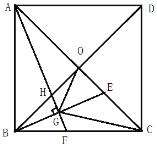
【题目】如图,在正方形ABCD中,对角线AC、BD相交于点O,E为OC上动点(不与O、C重合),作AF⊥BE,垂足为G,分别交BC、OB于F、H,连接OG、CG.
(1)求证:AH=BE;
(2)∠AGO的度数是否为定值?说明理由;
(3)若∠OGC=90°,BG=![]() ,求△OGC的面积.
,求△OGC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com