
【题目】如图,正六边形![]() 的对称中心
的对称中心![]() 在反比例函数
在反比例函数![]() (
(![]() ,
,![]() )的图象上,边
)的图象上,边![]() 在
在![]() 轴上,点
轴上,点![]() 在
在![]() 轴上,已知
轴上,已知![]() .
.
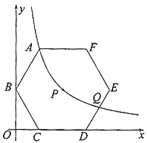
(1)点![]() 是否在该反比例函数的图象上?请说明理由;
是否在该反比例函数的图象上?请说明理由;
(2)若该反比例函数图象与![]() 交于点
交于点![]() ,求点
,求点![]() 的横坐标;
的横坐标;
(3)平移正六边形![]() ,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.
,使其一边的两个端点恰好都落在该反比例函数的图象上,试描述平移过程.
【答案】(1)点![]() 在该反比例函数的图像上,理由见解析;(2)
在该反比例函数的图像上,理由见解析;(2)![]() ;(3)答案见解析.
;(3)答案见解析.
【解析】
(1)过点P作x轴垂线PH,连接PC,可得PC=4,C是OH的中点,所以![]() ;
;
(2)易求D(6,0),设![]() ,则
,则![]() ,求得
,求得![]() 代入反比例函数解析式求得b的值即可得解;
代入反比例函数解析式求得b的值即可得解;
(3)求得正六边形![]() 各顶点坐标,根据平移性质即可得其一边的两个端点恰好都落在该反比例函数的图象上.
各顶点坐标,根据平移性质即可得其一边的两个端点恰好都落在该反比例函数的图象上.
(1)如图,连结![]() ,过点
,过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
∵在正六边形![]() 中,点
中,点![]() 在
在![]() 轴上,
轴上,
∴![]() 和
和![]() 都是含有
都是含有![]() 角的直角三角形,
角的直角三角形,
![]() ,
,
∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵点![]() 在反比例函数
在反比例函数![]() 上,
上,
∴反比例函数解析式为:![]() (
(![]() ),
),
连结![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,
,
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴点![]() 在该反比例函数的图像上.
在该反比例函数的图像上.

(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,
,
∵六边形![]() 为正六边形,
为正六边形,
∴![]() ,
,
设![]() ,则
,则![]() ,
,
∴![]() ,
,
又∵点![]() 在反比例函数上,
在反比例函数上,
∴![]() ,
,
解得:![]() ,
,![]() (舍去),
(舍去),
∴![]() ,
,
∴点![]() 的横坐标为
的横坐标为![]()

(3)易求A(2,4![]() ),B(0,2
),B(0,2![]() ),C(2,0),D(6,0),E(8,2
),C(2,0),D(6,0),E(8,2![]() ),F(6,4
),F(6,4![]() ),
),
设正六边形向左平移m个单位,向上平移n个单位,则平移后点的坐标分别为
∴A(2-m,4![]() +n),B(-m,2
+n),B(-m,2![]() +n),C(2-m,n),D(6-m,n),E(8-m,2
+n),C(2-m,n),D(6-m,n),E(8-m,2![]() +n),F(6-m,2
+n),F(6-m,2![]() +n),
+n),
①将正六边形向左平移4个单位后,E(4,2![]() ),F(2,4
),F(2,4![]() ),则点E与F都在反比例函数图象上;
),则点E与F都在反比例函数图象上;
②将正六边形向右平移2个单位,再向上平移2![]() 个单位后,C(4,2
个单位后,C(4,2![]() ),B(2,4
),B(2,4![]() ),则点B与C都在反比例函数图象上.
),则点B与C都在反比例函数图象上.


 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:初中数学 来源: 题型:
【题目】如图(1),某数学活动小组经探究发现:在⊙O中,直径AB与弦CD相交于点P,此时PA· PB=PC·PD
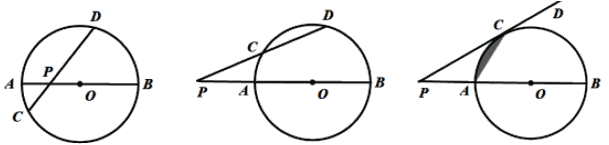
(1)如图(2),若AB与CD相交于圆外一点P, 上面的结论是否成立?请说明理由.
(2)如图(3),将PD绕点P逆时针旋转至与⊙O相切于点C, 直接写出PA、PB、PC之间的数量关系.
(3)如图(3),直接利用(2)的结论,求当 PC= ![]() ,PA=1时,阴影部分的面积.
,PA=1时,阴影部分的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明设计的“作等腰三角形外接圆”的尺规作图过程.
已知:如图1,在![]() 中,AB=AC.
中,AB=AC.
求作:等腰![]() 的外接圆.
的外接圆.

作法:
①如图2,作![]() 的平分线交BC于D ;
的平分线交BC于D ;
②作线段AB的垂直平分线EF;
③EF与AD交于点O;
④以点O为圆心,以OB为半径作圆.
所以,![]() 就是所求作的等腰
就是所求作的等腰![]() 的外接圆.
的外接圆.
根据小明设计的尺规作图过程,
(1)使用直尺和圆规,补全图形(保留痕迹);
(2)完成下面的证明.
![]() AB=AC,
AB=AC,![]() ,
,
![]() _________________________.
_________________________.
![]() AB的垂直平分线EF与AD交于点O,
AB的垂直平分线EF与AD交于点O,
![]() OA=OB,OB=OC
OA=OB,OB=OC
(填写理由:______________________________________)
![]() OA=OB=OC.
OA=OB=OC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 是线段
是线段![]() 的垂直平分线,交线段
的垂直平分线,交线段![]() 于点
于点![]() ,在
,在![]() 下方的直线
下方的直线![]() 上取一点
上取一点![]() ,连接
,连接![]() ,以线段
,以线段![]() 为边,在
为边,在![]() 上方作正方形
上方作正方形![]() ,射线
,射线![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
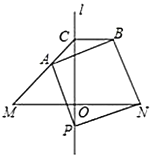
(1)设![]() ,求
,求![]() 的度数;
的度数;
(2)写出线段![]() 、
、![]() 之间的等量关系,并证明.
之间的等量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,反比例函数y=![]() (k≠0)的图象经过等腰△AOB底边OB的中点C和AB边上一点D,已知A(4,0),∠AOB=30°,则k的值为( )
(k≠0)的图象经过等腰△AOB底边OB的中点C和AB边上一点D,已知A(4,0),∠AOB=30°,则k的值为( )
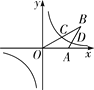
A.2![]() B.3
B.3![]() C.3D.4
C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某居民楼![]() 的前面有一围墙
的前面有一围墙![]() ,在点
,在点![]() 处测得楼顶
处测得楼顶![]() 的仰角为
的仰角为![]() ,在
,在![]() 处测得楼顶
处测得楼顶![]() 的仰角为
的仰角为![]() ,且
,且![]() 的高度为2米,
的高度为2米,![]() 之间的距离为20米(
之间的距离为20米(![]() ,
,![]() ,
,![]() 在同一条直线上).
在同一条直线上).
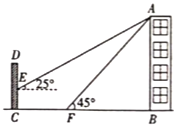
(1)求居民楼![]() 的高度.
的高度.
(2)请你求出![]() 、
、![]() 两点之间的距离.(参考数据:
两点之间的距离.(参考数据:![]() ,
,![]() ,
,![]() ,结果保留整数)
,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实立德树人的根本任务,加强思改、历史学科教师的专业化队伍建设.某校计划从前来应聘的思政专业(一名研究生,一名本科生)、历史专业(一名研究生、一名本科生)的高校毕业生中选聘教师,在政治思想审核合格的条件下,假设每位毕业生被录用的机会相等
(1)若从中只录用一人,恰好选到思政专业毕业生的概率是 :
(2)若从中录用两人,请用列表或画树状图的方法,求恰好选到的是一名思政研究生和一名历史本科生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,已知AB=AC,∠BAC=90°,E为边AC上一点,连接BE.
(1)如图1,若∠ABE=15°,O为BE中点,连接AO,且AO=1,求BC的长;
(2)如图2,D为AB上一点,且满足AE=AD,过点A作AF⊥BE交BC于点F,过点F作FG⊥CD交BE的延长线于点G,交AC于点M,求证:BG=AF+FG.
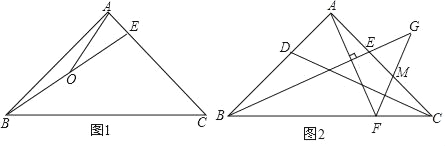
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com