
【题目】以点![]() 为顶点作等腰
为顶点作等腰![]() ,等腰
,等腰![]() ,其中
,其中![]() ,如图1所示放置,使得一直角边重合,连接
,如图1所示放置,使得一直角边重合,连接![]() 、
、![]() .
.
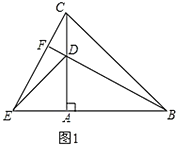
(1)试判断![]() 、
、![]() 的数量关系,并说明理由;
的数量关系,并说明理由;
(2)延长![]() 交
交![]() 于点
于点![]() 试求
试求![]() 的度数;
的度数;
(3)把两个等腰直角三角形按如图2放置,(1)、(2)中的结论是否仍成立?请说明理由.
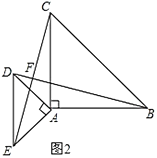
【答案】(1)BD=CE,理由见解析;(2)90°;(3)成立,理由见解析.
【解析】
(1)根据等腰直角三角形的性质得到AB=AC,∠BAD=∠EAC=90°,AD=AE,利用“SAS”可证明△ADB≌△AEC,则BD=CE;
(2)由△ADB≌△AEC得到∠ACE=∠DBA,利用三角形内角和定理可得到∠BFC=180°-∠ACE-∠CDF=180°-∠DBA-∠BDA=∠DAB=90°;
(3)与(1)一样可证明△ADB≌△AEC,得到BD=CE,∠ACE=∠DBA,利用三角形内角和定理得到∠BFC=∠DAB=90°.
(1)∵△ABC、△ADE是等腰直角三角形,
∴AB=AC,∠BAD=∠EAC=90°,AD=AE,
∵在△ADB和△AEC中,
|
∴△ADB≌△AEC(SAS),∴BD=CE;
(2)∵△ADB≌△AEC,∴∠ACE=∠ABD,
而在△CDF中,∠BFC=180°-∠ACE-∠CDF,
又∵∠CDF=∠BDA,
∴∠BFC=180°-∠DBA-∠BDA=∠DAB=90°;
(3)BD=CE成立,且两线段所在直线互相垂直,即∠BFC=90°.理由如下:
∵△ABC、△ADE是等腰直角三角形,
∴AB=AC,AD=AE,∠BAC=∠EAD=90°,
∵∠BAC+∠CAD=∠EAD+∠CAD,
∴∠BAD=∠CAE,
在△ADB和△AEC中,
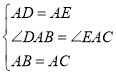 ,
,
∴△ADB≌△AEC(SAS),
∴BD=CE,∠ACE=∠DBA,
∴∠BFC=∠DAB=90°.


科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ABC=90°,AB=BC,直线l1、l2、l3分别通过A、B、C三点,且l1∥l2∥l3.若l1与l2的距离为5,l2与l3的距离为7,则Rt△ABC的面积为___________

查看答案和解析>>
科目:初中数学 来源: 题型:
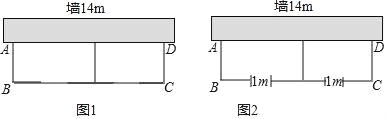
【题目】如图,有长为22米的篱笆,一面利用墙(墙的最大可用长度为14米),围成中间隔有一道篱笆的长方形花圃,有以下两种围法.
(1)如图1,设花圃的宽AB为x米,面积为y米2,求y与x之间的含函数表达式,并确定x的取值范围;
(2)如图2,为了方便出入,在建造篱笆花圃时,在BC上用其他材料造了宽为1米的两个小门,设花圃的宽AB为a米,面积为S米2,求S与a之间的函数表达式及S的最大值?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,过点C的直线MN∥AB,D为AB边上一点,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD,BE.
(1)求证:CE=AD;
(2)当D为AB中点时,四边形BECD是什么特殊四边形?说明你的理由;
(3)若D为AB中点,则当∠A的大小满足什么条件时,四边形BECD是正方形?请说明你的理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将两张完全相同的矩形纸片![]() 、
、![]() 按如图方式放置,
按如图方式放置,![]() 为重合的对角线.重叠部分为四边形
为重合的对角线.重叠部分为四边形![]() ,
,

![]() 试判断四边形
试判断四边形![]() 为何种特殊的四边形,并说明理由;
为何种特殊的四边形,并说明理由;
![]() 若
若![]() ,
,![]() ,求四边形
,求四边形![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
“ a 2 ≥0”这个结论在数学中非常有用,有时我们需要将代数式配成完全平方式.例如:
x2 4x 5 x2 4x 4 1 x 22 1 ,
∵ x 22 ≥0,
∴ x 22 1 ≥1,
∴ x2 4x 5 ≥1.
试利用“配方法”解决下列问题:
(1)填空: x2 4x 5 ( x )2+ ;
(2)已知 x2 4x y2 2y 5 0 ,求 x y 的值;
(3)比较代数式 x2 1与2x 3 的大小.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在△ABC中,AB=8cm,BC=16 cm.点P从点A出发沿AB向点B以2 cm/s的速度运动,点Q从点B出发沿BC向点C以4 cm/s的速度运动.如果点P,Q分别从点A,B同时出发,则_____________秒钟后△PBQ与△ABC相似?
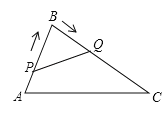
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某日王老师佩戴运动手环进行快走锻炼,两次锻炼后数据如表.与第一次锻炼相比,王老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.设王老师第二次锻炼时平均步长减少的百分率为![]() .
.
项目 | 第一次锻炼 | 第二次锻炼 |
步数(步) | 10000 | ____________ |
平均步长(米/步) | 0.6 | ____________ |
距离(米) | 6000 | 7020 |
注:步数×平均步长=距离.
(1)根据题意完成表格填空;
(2)求x;
(3)王老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求王老师这500米的平均步长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在Rt△ABC中,∠ACB=90°,AC=10cm,BC=5cm,点P从点C出发沿线段CA以每秒2cm的速度运动,同时点Q从点B出发沿线段BC以每秒1cm的速度运动.设运动时间为t秒(0<t<5).

(1)填空:AB= cm;
(2)t为何值时,△PCQ与△ACB相似;
(3)如图2,以PQ为斜边在异于点C的一侧作Rt△PEQ,且![]() ,连结CE,求CE.(用t的代数式表示).
,连结CE,求CE.(用t的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com