
(9分)(2014•昆明)如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3(a≠0)与x轴交于点A(﹣2,0)、B(4,0)两点,与y轴交于点C.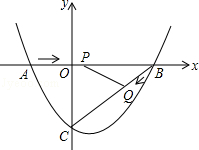
(1)求抛物线的解析式;
(2)点P从A点出发,在线段AB上以每秒3个单位长度的速度向B点运动,同时点Q从B点出发,在线段BC上以每秒1个单位长度的速度向C点运动,其中一个点到达终点时,另一个点也停止运动,当△PBQ存在时,求运动多少秒使△PBQ的面积最大,最大面积是多少?
(3)当△PBQ的面积最大时,在BC下方的抛物线上存在点K,使S△CBK:S△PBQ=5:2,求K点坐标.
(1)y= x2﹣
x2﹣ x﹣3
x﹣3
(2)运动1秒使△PBQ的面积最大,最大面积是
(3)K1(1,﹣ ),K2(3,﹣
),K2(3,﹣ )
)
解析试题分析:(1)把点A、B的坐标分别代入抛物线解析式,列出关于系数a、b的解析式,通过解方程组求得它们的值;
(2)设运动时间为t秒.利用三角形的面积公式列出S△PBQ与t的函数关系式S△PBQ=﹣ (t﹣1)2+
(t﹣1)2+ .利用二次函数的图象性质进行解答;
.利用二次函数的图象性质进行解答;
(3)利用待定系数法求得直线BC的解析式为y= x﹣3.由二次函数图象上点的坐标特征可设点K的坐标为(m,
x﹣3.由二次函数图象上点的坐标特征可设点K的坐标为(m, m2﹣
m2﹣ m﹣3).
m﹣3).
如图2,过点K作KE∥y轴,交BC于点E.结合已知条件和(2)中的结果求得S△CBK= .则根据图形得到:S△CBK=S△CEK+S△BEK=
.则根据图形得到:S△CBK=S△CEK+S△BEK= EK•m+
EK•m+ •EK•(4﹣m),把相关线段的长度代入推知:﹣
•EK•(4﹣m),把相关线段的长度代入推知:﹣ m2+3m=
m2+3m= .易求得K1(1,﹣
.易求得K1(1,﹣ ),K2(3,﹣
),K2(3,﹣ ).
).
解:(1)把点A(﹣2,0)、B(4,0)分别代入y=ax2+bx﹣3(a≠0),得 ,
,
解得  ,
,
所以该抛物线的解析式为:y= x2﹣
x2﹣ x﹣3;
x﹣3;
(2)设运动时间为t秒,则AP=3t,BQ=t.
∴PB=6﹣3t.
由题意得,点C的坐标为(0,﹣3).
在Rt△BOC中,BC= =5.
=5.
如图1,过点Q作QH⊥AB于点H.
∴QH∥CO,
∴△BHQ∽△BOC,
∴ =
= ,即
,即 =
= ,
,
∴HQ= t.
t.
∴S△PBQ= PB•HQ=
PB•HQ= (6﹣3t)•
(6﹣3t)• t=﹣
t=﹣ t2+
t2+ t=﹣
t=﹣ (t﹣1)2+
(t﹣1)2+ .
.
当△PBQ存在时,0<t<2
∴当t=1时,
S△PBQ最大= .
.
答:运动1秒使△PBQ的面积最大,最大面积是 ;
;
(3)设直线BC的解析式为y=kx+c(k≠0).
把B(4,0),C(0,﹣3)代入,得 ,
,
解得  ,
,
∴直线BC的解析式为y= x﹣3.
x﹣3.
∵点K在抛物线上.
∴设点K的坐标为(m, m2﹣
m2﹣ m﹣3).
m﹣3).
如图2,过点K作KE∥y轴,交BC于点E.则点E的坐标为(m, m﹣3).
m﹣3).
∴EK= m﹣3﹣(
m﹣3﹣( m2﹣
m2﹣ m﹣3)=﹣
m﹣3)=﹣ m2+
m2+ m.
m.
当△PBQ的面积最大时,∵S△CBK:S△PBQ=5:2,S△PBQ= .
.
∴S△CBK= .
.
S△CBK=S△CEK+S△BEK= EK•m+
EK•m+ •EK•(4﹣m)
•EK•(4﹣m)
= ×4•EK
×4•EK
=2(﹣ m2+
m2+ m)
m)
=﹣ m2+3m.
m2+3m.
即:﹣ m2+3m=
m2+3m= .
.
解得 m1=1,m2=3.
∴K1(1,﹣ ),K2(3,﹣
),K2(3,﹣ ).
).
点评:本题是二次函数的综合题型,其中涉及到的知识点有待定系数法求二次函数解析式和三角形的面积求法.在求有关动点问题时要注意该点的运动范围,即自变量的取值范围.


科目:初中数学 来源: 题型:解答题
一根80厘米的弹簧,一端固定,如果另一端挂上物体,那么在正常情况下物体的质量每增加1千克可使弹簧增长2厘米。(10 分)
(1)填写下表
| 所挂物体的质量(千克) | 1 | 2 | 3 | 4 | … |
| 弹簧的总长度(厘米) | | | | | … |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(本题8分)如图表示一个正比例函数与一个一次函数的图象,它们交于点A(4,3),一次函数的图象与y轴交于点B,且OA=OB,求这两个函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
(本小题满分10分)如图,抛物线 与
与 轴交
轴交 、
、 两点,直线
两点,直线 与抛物线交于A、C两点,其中C点的横坐标为2.
与抛物线交于A、C两点,其中C点的横坐标为2.
(1)求抛物线及直线AC的函数表达式;
(2)若P点是线段AC上的一个动点,过P点作 轴的平行线交抛物线于F点,求线段PF长度的最大值.
轴的平行线交抛物线于F点,求线段PF长度的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
已知抛物线抛物线y n=-(x-an)2+an(n为正整数,且0<a1<a2<…<an)与x轴的交点为An-1(bn-1,0)和An(bn,0),当n=1时,第1条抛物线y1=-(x-a1)2+a1与x轴的交点为A0(0,0)和A1(b1,0),其他依此类推.
(1)求a1,b1的值及抛物线y2的解析式;
(2)抛物线y3的顶点坐标为( , );
依此类推第n条抛物线yn的顶点坐标为( , );
所有抛物线的顶点坐标满足的函数关系是 ;
(3)探究下列结论:
若用An-1An表示第n条抛物线被x轴截得得线段长,直接写出A0A1的值,并求出An-1An;
查看答案和解析>>
科目:初中数学 来源: 题型:单选题
多多班长统计去年1~8月“书香校园”活动中全班同学的课外阅读数量(单位:本),绘制了如图折线统计图,下列说法正确的是( )
| A.极差是47 |
| B.众数是42 |
| C.中位数是58 |
| D.每月阅读数量超过40的有4个月 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com