
分析 (1)①根据二次函数的图象与x轴只有一个交点,则(2b)2-4c=0,由此可得到b、c 应满足关系;
②把y=9代入y=x2-2bx+bc,得到方程x2-2bx+bc-9=0,根据根与系数的关系和①的结论即可求得;
③把A(m,n)、B(m+4,n)分别代入抛物线的解析式,再根据①的结论即可求出n的值;
(2)①因为y=x2-2bx+c图象与x轴交于E(5,0),即可得到25-10b+c=0,所以c=10b-25;
②根据①的距离进而得到k=2b-5,再根据E、F之间的整数和为18,即可求出k的取值范围和b的值.
解答 解:(1)①∵二次函数y=x2-2bx+c的图象与x轴只有一个交点,
∴(2b)2-4c=0,
∴b2=c;
故答案为b2=c;
②把y=9代入y=x2-2bx+c得,9=x2-2bx+c,
∴x2-2bx+c-9=0,
∵x1+x2=2b,x1x2=c-9,
∴(x1-x2)2=(x1+x2)2-4x1x2=(2b)2-4(c-9)=36,
∴|AB|=|x1-x2|=6;
故答案为6;
③|CD|=|xC-xD|=|m-(m+4)|=4,
∵m+4)2-2b(m+4)+b2,解得b=m+2,
代入n=m2-2bm+b2,解得n=4;
(2)①∵y=x2-2bx+c图象与x轴交于E(5,0)
∴25-10b+c=0,
∴c=10b-25;
故答案为c=10b-25;
②∵c=10b-25,
∴y=x2-2bx+c=10b-25,令y=0得x2-2bx+10b-25=0
解得:x1=5,x2=2b-5,即k=2b-5;
∵整数和为18,则7≤k<8,
∴k=7,
∴7=2b-5,解得b=6.
故答案为7≤k<8,6.
点评 本题是二次函数的综合题型,主要考查了根的判别式,二次函数与x轴的交点问题,二次函数与不等式的关系,题目的综合性较强,难度不小,对学生的解题能力要求很高,是一道不错的中考压轴题.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:选择题
| A. | 抛物线开口向上 | |
| B. | 抛物线的对称轴是x=1 | |
| C. | 当x=1时,y的最大值为-4 | |
| D. | 关于x的一元二次方程x2-2x+c的两个根为-1,3 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
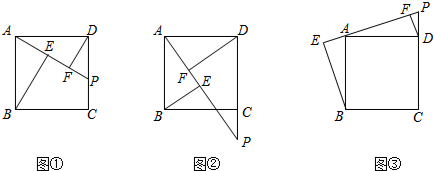
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
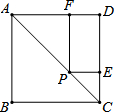 如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )
如图,在正方形ABCD中,对角线AC=6,点P是对角线AC上的一点,过点P作PF⊥AD,PE⊥CD,则PF+PE的值为( )| A. | 3$\sqrt{2}$ | B. | 3 | C. | 2$\sqrt{3}$ | D. | 6 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
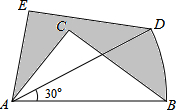 如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积为( )
如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积为( )| A. | $\frac{25}{12}$π | B. | $\frac{4}{3}$π | C. | $\frac{3}{4}$π | D. | $\frac{5}{12}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
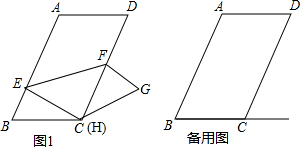
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| x(件) | … | 5 | 10 | 15 | 20 | … |
| y(元/件) | … | 75 | 70 | 65 | 60 | … |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com