
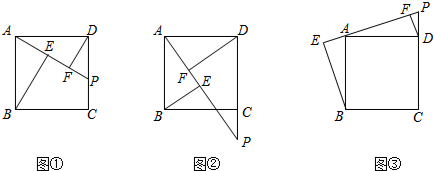
分析 (1)DE+EF=BE.根据正方形的性质,证明△DAF≌△ABE即可;
(2)DE-EF=BE.运用类比思想,根据正方形的性质,证明△DAF≌△ABE即可;
(3)EF=BE+DF.证明方法类比(1)、(2).
解答 解:(1)DE+EF=BE,理由如下:
在正方形ABCD中,AB=AD,∠BAD=90°,
即∠BAE+∠EAD=90°,
∵BE⊥PA,
∴∠BAE+∠ABE=90°,
∴∠ABE=∠EAD,
∵BE⊥PA,DF⊥PA,
∴∠AEB=∠DFA=90°,
在△AEB和△DFA中,
$\left\{\begin{array}{l}{∠ABE=∠EAD}\\{∠AEB=∠DFA}\\{AB=AD}\end{array}\right.$,
∴△DAF≌△ABE,
∴AE=DF,BE=AF
∴DF+EF=AE+EF=AF=BE,即DE+EF=BE.
(2)DE-EF=BE,理由如下:
在正方形ABCD中AB=AD,∠BAD=90°,
即∠BAE+∠EAD=90°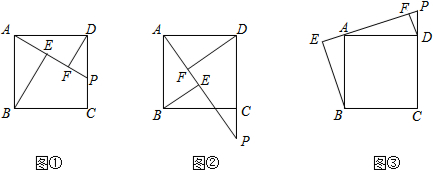
∵BE⊥PA,
∴∠BAE+∠ABE=90°,
∴∠ABE=∠EAD,
∵BE⊥PA,DF⊥PA
∴∠AEB=∠DFA=90°,
在△AEB和△DFA中,
$\left\{\begin{array}{l}{∠ABE=∠EAD}\\{∠AEB=∠DFA}\\{AB=AD}\end{array}\right.$,
∴△DAF≌△ABE,
∴AE=DF,BE=AF,
∵AE-EF=AF,即DE-EF=BE;
(3)EF=BE+DF.
理由如下:
在正方形ABCD中,AB=AD,∠BAD=90°,
即∠BAE+∠FAD=90°
∵BE⊥PA,
∴∠BAE+∠ABE=90°,
∴∠ABE=∠FAD,
∵BE⊥PA,DF⊥PA
∴∠AEB=∠DFA=90°,
在△AEB和△DFA中,
$\left\{\begin{array}{l}{∠ABE=∠FAD}\\{∠AEB=∠DFA}\\{AB=AD}\end{array}\right.$,
∴△DAF≌△ABE,
∴AE=DF,BE=AF,
∵EF=AF+AE,
∴EF=BE+DF.
点评 本题主要考查了正方形的性质、全等三角形的判定与性质,运用类比思想,在变化中发现不变是解决问题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 从2013年1月7日起,中国中东部大部分地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.
从2013年1月7日起,中国中东部大部分地区持续出现雾霾天气,某市记者为了了解“雾霾天气的主要成因”,随机调查了该市部分市民,并对调查结果进行整理,绘制了如下尚不完整的统计图表.| 组别 | 观点 | 频数(人数) |
| A | 大气气压低,空气不流动 | 80 |
| B | 地面灰尘大,空气湿度低 | m |
| C | 汽车尾气排放 | n |
| D | 工厂造成污染 | 120 |
| E | 其他 | 60 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
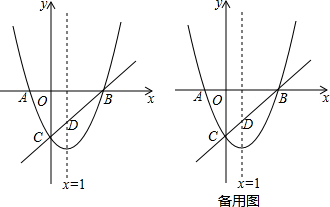
 如图,抛物线y=x2+bx+c与x轴交于A(-2,0),B(6,0)两点,与y轴交于点C,请解答下列问题:
如图,抛物线y=x2+bx+c与x轴交于A(-2,0),B(6,0)两点,与y轴交于点C,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
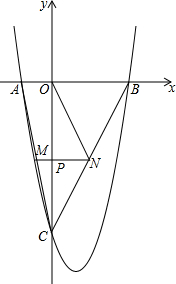
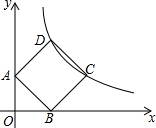 如图,正方形ABCD的顶点A、B分别在y正半轴和x正半轴上,顶点C、D在第一象限内反比例函数y=$\frac{k}{x}$的图象上.
如图,正方形ABCD的顶点A、B分别在y正半轴和x正半轴上,顶点C、D在第一象限内反比例函数y=$\frac{k}{x}$的图象上.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com