
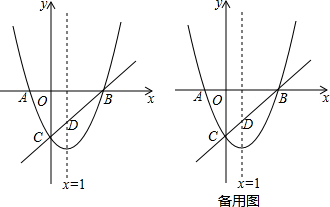
���� ��1�����������ߵĶԳ��᷽�̿ɼ����b=-2���ٰ�C��0��-3�����������߽���ʽ�ɵõ�c=-3�����������ߵĺ�������ʽΪy=x2-2x-3��
��2��������������x��Ľ�������õ�A��-1��0����B��3��0����Ȼ�����ô���ϵ�������ֱ��BC�ĺ�������ʽ��
��3������AB=4��PQ=$\frac{3}{4}$AB=3�����������ߵĶԳ��Եõ�P���Q�����ֱ��x=1�Գƣ���P��-$\frac{1}{2}$��-$\frac{7}{4}$��������F��0��-$\frac{7}{4}$������FC=3-OF=$\frac{5}{4}$������PQ��ֱƽ��CE�ڵ�F����CE=2FC=$\frac{5}{2}$����D��1��-2��������D��DG��CE�ڵ�G����ͼ1����DG=1��CG=1������GE=CE=CG=$\frac{3}{2}$��Ȼ����Rt��EGD�У��������еĶ�����⣻
����E��0��t�������������ľ��빫ʽ�õ�DE2=12+��t+2��2��CD2=12+��-2+3��2=2��EC2=��t+3��2��Ȼ��������ۣ�����CDE=90��ʱ��DE2+CD2=EC2����12+��t+2��2+2=��t+3��2������CED=90��ʱ��DE2+CE2=CD2����12+��t+2��2+��t+3��2=2������ECD=90��ʱ��CD2+CE2=DE2����2+��t+3��2=12+��t+2��2���ٷֱ�ⷽ�����tȷ��E�����꣬Ȼ����ݶ��κ���ͼ���ϵ����������ȷ��P�����꣮
��� �⣺��1���������ߵĶԳ�����ֱ��x=1
��-$\frac{b}{2}$=1�����b=-2��
��������y�ύ�ڵ�C��0��-3����
��c=-3��
�������ߵĺ�������ʽΪy=x2-2x-3��
��2����y=0ʱ��x2-2x-3=0�����x1=-1��x2=3����A��-1��0����B��3��0����
��ֱ��BC�ĺ�������ʽΪy=kx+m��
��C��0��-3����B��3��0���ֱ�����$\left\{\begin{array}{l}{m=-3}\\{3k+m=0}\end{array}\right.$�����$\left\{\begin{array}{l}{k=1}\\{m=-3}\end{array}\right.$��
��ֱ��BC�ĺ�������ʽΪy=x-3��
��3���١�AB=4��
��PQ=$\frac{3}{4}$AB=3��
��PQ��y�ᣬ
��PQ��x�ᣬ
��P���Q�����ֱ��x=1�Գƣ�
��P��ĺ�����Ϊ-$\frac{1}{2}$��
��x=-$\frac{1}{2}$ʱ��y=x2-2x-3=-$\frac{7}{4}$��
��P��-$\frac{1}{2}$��-$\frac{7}{4}$����
��F��0��-$\frac{7}{4}$����
��FC=3-OF=3-$\frac{7}{4}$=$\frac{5}{4}$��
��PQ��ֱƽ��CE�ڵ�F��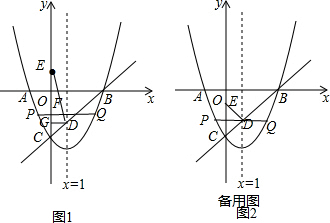
��CE=2FC=$\frac{5}{2}$��
�൱x=1ʱ��y=-2����D��1��-2����
����D��DG��CE�ڵ�G����ͼ1��
��DG=1��CG=1��
��GE=CE=CG=$\frac{5}{2}$-1=$\frac{3}{2}$��
��Rt��EGD��tan��CED=$\frac{DG}{EG}$=$\frac{1}{\frac{3}{2}}$=$\frac{2}{3}$��
����E��0��t����
DE2=12+��t+2��2��CD2=12+��-2+3��2=2��EC2=��t+3��2��
����CDE=90��ʱ��DE2+CD2=EC2����12+��t+2��2+2=��t+3��2�����t=-1����ʱP��1-2$\sqrt{2}$��-2����
����CED=90��ʱ��DE2+CE2=CD2����12+��t+2��2+��t+3��2=2�����t1=-2��t2=-3����ȥ������ʱP��1-$\frac{\sqrt{6}}{2}$��-$\frac{5}{2}$����
����ECD=90��ʱ��CD2+CE2=DE2����2+��t+3��2=12+��t+2��2�����t=-3����ȥ����
����������P��������1-$\sqrt{2}$��-2����1-$\frac{\sqrt{6}}{2}$��-$\frac{5}{2}$����
���� ���⿼���˶��κ������ۺ��⣺�������ն��κ���ͼ���ϵ�����������Ͷ��κ��������ʣ������ô���ϵ�����������߽���ʽ������������ͼ�ε����ʣ������������ľ��빫ʽ�����߶εij���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
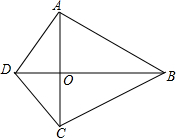 ��֪����ͼ���ı���ABCD�У�AB=CB=40��AD=CD=30��
��֪����ͼ���ı���ABCD�У�AB=CB=40��AD=CD=30���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ���ڽǶ����� | B�� | �Խ�����ƽ�� | ||
| C�� | �����Խ������ | D�� | ����ԽǷֱ���� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
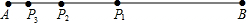
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
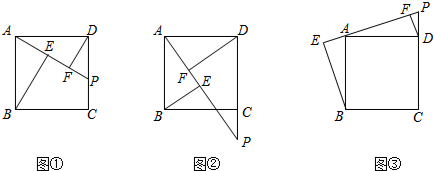
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����Rt��ABC�У���C=90�㣬ֱ��DE��б��AB�Ĵ�ֱƽ���߽�AC��D����AC=8��BC=6�����DBC���ܳ�Ϊ��������
��ͼ����Rt��ABC�У���C=90�㣬ֱ��DE��б��AB�Ĵ�ֱƽ���߽�AC��D����AC=8��BC=6�����DBC���ܳ�Ϊ��������| A�� | 12 | B�� | 14 | C�� | 16 | D�� | ������ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com