
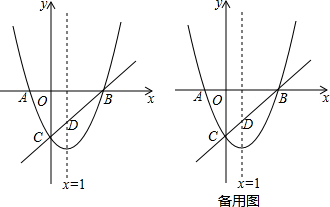
 如图,在Rt△ABC中,∠C=90°,直线DE是斜边AB的垂直平分线交AC于D.若AC=8,BC=6,则△DBC的周长为( )
如图,在Rt△ABC中,∠C=90°,直线DE是斜边AB的垂直平分线交AC于D.若AC=8,BC=6,则△DBC的周长为( )| A. | 12 | B. | 14 | C. | 16 | D. | 无法计算 |
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
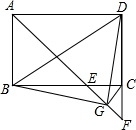 如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:
如图,在矩形ABCD中,∠BAD的平分线交BC于点E,交DC的延长线于点F,取EF的中点G,连接CG,BG,BD,DG,下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
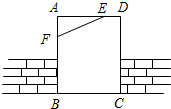 如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )
如图,工人师傅砌门时,常用木条EF固定长方形门框ABCD,使其不变形,这样做的根据是( )| A. | 两点之间,线段最短 | B. | 直角三角形的两个锐角互余 | ||
| C. | 三角形三个内角和等于180° | D. | 三角形具有稳定性 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
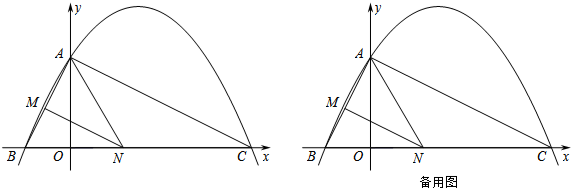
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $\frac{900}{m}=\frac{750}{m+3}$ | B. | $\frac{900}{m+3}=\frac{750}{m}$ | C. | $\frac{900}{m}=\frac{750}{m-3}$ | D. | $\frac{900}{m-3}=\frac{750}{m}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
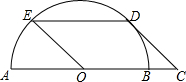 如图,点C是半圆O的直径AB的延长线上一点.CD与半圆O相切,D为切点,过点D作DE∥AB交半圆O于点E.若四边形OCDE是平行四边形,CD=4,则ED的长为( )
如图,点C是半圆O的直径AB的延长线上一点.CD与半圆O相切,D为切点,过点D作DE∥AB交半圆O于点E.若四边形OCDE是平行四边形,CD=4,则ED的长为( )| A. | 4 | B. | 4$\sqrt{2}$ | C. | 2$\sqrt{6}$ | D. | 3$\sqrt{3}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com