
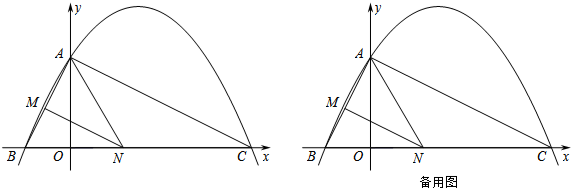
���� ��1�����ݴ���ϵ����������ã�
��2�����������ߵĽ���ʽ���B�����꣬Ȼ����ݹ��ɶ����ֱ����AB2=20��AC2=80��BC10��Ȼ����ݹ��ɶ������涨������֤�á�ABC��ֱ�������Σ�
��3���ֱ���A��C����ΪԲ�ģ�AC��Ϊ�뾶��������x�ύ�������㣬��AC�Ĵ�ֱƽ������x�ύ��һ���㣬������õ�N�����ꣻ
��4�����N������Ϊ��n��0������BN=n+2����M����MD��x���ڵ�D���������������ƶ�Ӧ�߳ɱ������MD=$\frac{2}{5}$��n+2����Ȼ�����S��AMN=S��ABN-S��BMN
�ó�����n�Ķ��κ��������ݺ�������ʽ��ü��ɣ�
��� 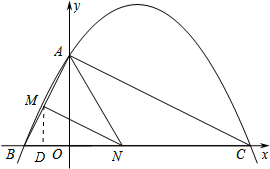 �⣺��1���߶��κ���y=ax2+$\frac{3}{2}$x+c��ͼ����y�ύ�ڵ�A��0��4������x�ύ�ڵ�B��C����C����Ϊ��8��0����
�⣺��1���߶��κ���y=ax2+$\frac{3}{2}$x+c��ͼ����y�ύ�ڵ�A��0��4������x�ύ�ڵ�B��C����C����Ϊ��8��0����
��$\left\{\begin{array}{l}{c=4}\\{64a+12+c=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=-\frac{1}{4}}\\{c=4}\end{array}\right.$��
�������߱���ʽ��y=-$\frac{1}{4}$x2+$\frac{3}{2}$x+4��
��2����ABC��ֱ�������Σ�
��y=0����-$\frac{1}{4}$x2+$\frac{3}{2}$x+4=0��
���x1=8��x2=-2��
���B��������-2��0����
����֪�ɵã�
��Rt��ABO��AB2=BO2+AO2=22+42=20��
��Rt��AOC��AC2=AO2+CO2=42+82=80��
�֡�BC=OB+OC=2+8=10��
���ڡ�ABC��AB2+AC2=20+80=102=BC2
���ABC��ֱ�������Σ�
��3����A��0��4����C��8��0����
��AC=$\sqrt{{4}^{2}+{8}^{2}}$=4$\sqrt{5}$��
����AΪԲ�ģ���AC��Ϊ�뾶��Բ����x����N����ʱN������Ϊ��-8��0����
����CΪԲ�ģ���AC��Ϊ�뾶��Բ����x����N����ʱN������Ϊ��8-4$\sqrt{5}$��0����8+4$\sqrt{5}$��0��
����AC�Ĵ�ֱƽ���ߣ���x����N����ʱN������Ϊ��3��0����
���ϣ�����N��x�����˶������Ե�A��N��CΪ������������ǵ���������ʱ����N������ֱ�Ϊ��-8��0������8-4$\sqrt{5}$��0������3��0������8+4$\sqrt{5}$��0����
��4�����N������Ϊ��n��0������BN=n+2����M����MD��x���ڵ�D��
��MD��OA��
���BMD�ס�BAO��
��$\frac{BM}{BA}$=$\frac{MD}{OA}$��
��MN��AC
��$\frac{BM}{BA}$=$\frac{BN}{BC}$��
��$\frac{MD}{OA}$=$\frac{BN}{BC}$��
��OA=4��BC=10��BN=n+2
��MD=$\frac{2}{5}$��n+2����
��S��AMN=S��ABN-S��BMN
=$\frac{1}{2}$BN•OA-$\frac{1}{2}$BN•MD
=$\frac{1}{2}$��n+2����4-$\frac{1}{2}$��$\frac{2}{5}$��n+2��2
=-$\frac{1}{5}$��n-3��2+5��
�൱��AMN������ʱ��N������Ϊ��3��0����
���� �����Ƕ��κ������ۺ��⣬�����˴���ϵ���������ʽ�����ɶ������涨�������������ε����ʣ����������Ƶ��ж��������Լ���������ֵ�ȣ������������ʶ����ǽ���Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��ƫ��60�� | B�� | ��ƫ��30�� | C�� | ��ƫ��30�� | D�� | ��ƫ��60�� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 ��ͼ����Rt��ABC�У���C=90�㣬ֱ��DE��б��AB�Ĵ�ֱƽ���߽�AC��D����AC=8��BC=6�����DBC���ܳ�Ϊ��������
��ͼ����Rt��ABC�У���C=90�㣬ֱ��DE��б��AB�Ĵ�ֱƽ���߽�AC��D����AC=8��BC=6�����DBC���ܳ�Ϊ��������| A�� | 12 | B�� | 14 | C�� | 16 | D�� | ������ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com