
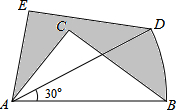
 如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积为( )
如图,在△ABC中,AB=5,AC=3,BC=4,将△ABC绕点A逆时针旋转30°后得到△ADE,点B经过的路径为$\widehat{BD}$,则图中阴影部分的面积为( )| A. | $\frac{25}{12}$π | B. | $\frac{4}{3}$π | C. | $\frac{3}{4}$π | D. | $\frac{5}{12}$π |
分析 根据AB=5,AC=3,BC=4和勾股定理的逆定理判断三角形的形状,根据旋转的性质得到△AED的面积=△ABC的面积,得到阴影部分的面积=扇形ADB的面积,根据扇形面积公式计算即可.
解答 解:∵AB=5,AC=3,BC=4,
∴△ABC为直角三角形,
由题意得,△AED的面积=△ABC的面积,
由图形可知,阴影部分的面积=△AED的面积+扇形ADB的面积-△ABC的面积,
∴阴影部分的面积=扇形ADB的面积=$\frac{30π×{5}^{2}}{360}$=$\frac{25}{12}π$,
故选:A.
点评 本题考查的是扇形面积的计算、旋转的性质和勾股定理的逆定理,根据图形得到阴影部分的面积=扇形ADB的面积是解题的关键.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:初中数学 来源: 题型:填空题
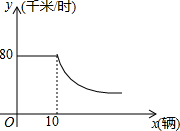 随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当x≥10时,y与x成反比例函数关系,当车速度低于20千米/时,交通就会拥堵,为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是0<x≤40.
随着私家车的增加,城市的交通也越来越拥挤,通常情况下,某段高架桥上车辆的行驶速度y(千米/时)与高架桥上每百米拥有车的数量x(辆)的关系如图所示,当x≥10时,y与x成反比例函数关系,当车速度低于20千米/时,交通就会拥堵,为避免出现交通拥堵,高架桥上每百米拥有车的数量x应该满足的范围是0<x≤40.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
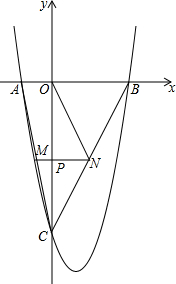 如图,抛物线y=x2+bx+c与x轴交于A(-2,0),B(6,0)两点,与y轴交于点C,请解答下列问题:
如图,抛物线y=x2+bx+c与x轴交于A(-2,0),B(6,0)两点,与y轴交于点C,请解答下列问题:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D.
已知抛物线y=x2+bx+c经过A(-1,0),B(3,0)两点,与y轴相交于点C,该抛物线的顶点为点D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 同位角相等,两条直线平行 | B. | 三条线段可以组成一个三角形 | ||
| C. | 平行于同一条直线的两条直线平行 | D. | 对顶角相等 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com