
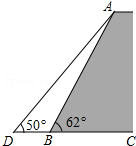
 如图,一堤坝的坡角∠ABC=62°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到1米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20)
如图,一堤坝的坡角∠ABC=62°,坡面长度AB=30米(图为横截面),为了使堤坝更加牢固,一施工队欲改变堤坝的坡面,使得坡面的坡角∠ADB=50°,则此时应将坝底向外拓宽多少米?(结果保留到1米)(参考数据:sin62°≈0.88,cos62°≈0.47,tan50°≈1.20) 分析 过A点作AE⊥CD于E.在Rt△ABE中,根据三角函数可得AE,BE,在Rt△ADE中,根据三角函数可得DE,再根据DB=DC-BE即可求解.
解答 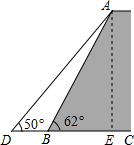 解:过A点作AE⊥CD于E.
解:过A点作AE⊥CD于E.
在Rt△ABE中,∠ABE=62°.
∴AE=AB•sin62°=30×0.88=26.4米,
BE=AB•cos62°=30×0.47=14米,
在Rt△ADE中,∠ADB=50°,
∴DE=$\frac{AE}{tan50°}$=22米,
∴DB=DE-BE≈8米.
故此时应将坝底向外拓宽大约8米.
点评 考查了解直角三角形的应用-坡度坡角问题,两个直角三角形有公共的直角边,先求出公共边的解决此类题目的基本出发点.


 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案科目:初中数学 来源: 题型:选择题
| A. | y3<y2<y1 | B. | y2<y1<y3 | C. | y1<y2<y3 | D. | y2<y3<y1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
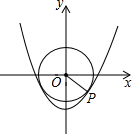 如图,已知二次函数的解析式为y=x2-1,其图象上有一个动点P,连接OP(O为坐标原点),并以OP为半径作圆,则该圆的最小面积是( )
如图,已知二次函数的解析式为y=x2-1,其图象上有一个动点P,连接OP(O为坐标原点),并以OP为半径作圆,则该圆的最小面积是( )| A. | $\frac{1}{2}$π | B. | $\frac{3}{4}$π | C. | π | D. | $\frac{9}{16}$π |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
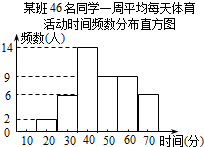 某班体育委员调查了本班46名同学一周的平均每天体育活动时间,并制作了如图所示的频数分布直方图,从直方图中可以看出,该班同学这一周平均每天体育活动时间的中位数在第4组,众数依次是在第3组.(从左至右数)
某班体育委员调查了本班46名同学一周的平均每天体育活动时间,并制作了如图所示的频数分布直方图,从直方图中可以看出,该班同学这一周平均每天体育活动时间的中位数在第4组,众数依次是在第3组.(从左至右数)查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 正数 | B. | 负数 | C. | 非正数 | D. | 非负数 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com