
科目:初中数学 来源: 题型:选择题
| A. | y=(x-1)2+1 | B. | y=(x+1)2+1 | C. | y=(x-1)2-3 | D. | y=(x+1)2+3 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | y1<0<y2 | B. | y2<0<y1 | C. | y1<y2<0 | D. | y2<y1<0 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE=$\frac{1}{2}$.
如图,在?ABCD中,AE⊥BC,垂足为E,如果AB=5,BC=8,sinB=$\frac{4}{5}$,那么tan∠CDE=$\frac{1}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 关于x的方程kx2+(3k+1)x+3=0.
关于x的方程kx2+(3k+1)x+3=0.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 3m=3n | B. | $\frac{m}{4}$=$\frac{n}{4}$ | C. | -m+2=-n+2 | D. | m+1=n-1 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
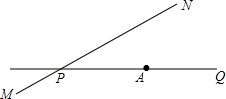 霾,也称阴霾、灰霾,是指原因不明的大量烟、尘等微粒悬浮而形成的浑浊现象.霾的核心物质是空气中悬浮的灰尘颗粒,气象学上称为气溶胶颗粒.随着中国社会的经济发展水平越来越高,越来越多的城市受雾霾影响.公路MN和公路PQ在点P处交汇,且∠QPN=30°,辰宇图象在点A处等公共汽车,AP=160m,一辆洒水车以3.6km/h的速度在公路MN上沿PN方向行驶,由于有霾,当时能见度只有100米,那么,辰宇同学能否会看到洒水车?如果不能看到,请说明理由;如果能看到,能看到几分钟?
霾,也称阴霾、灰霾,是指原因不明的大量烟、尘等微粒悬浮而形成的浑浊现象.霾的核心物质是空气中悬浮的灰尘颗粒,气象学上称为气溶胶颗粒.随着中国社会的经济发展水平越来越高,越来越多的城市受雾霾影响.公路MN和公路PQ在点P处交汇,且∠QPN=30°,辰宇图象在点A处等公共汽车,AP=160m,一辆洒水车以3.6km/h的速度在公路MN上沿PN方向行驶,由于有霾,当时能见度只有100米,那么,辰宇同学能否会看到洒水车?如果不能看到,请说明理由;如果能看到,能看到几分钟?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com