
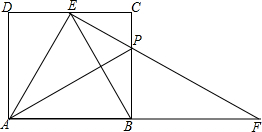
 如图,在矩形ABCD中,AB=2,AD=$\sqrt{3}$,在边CD上有一点E,使EB平分∠AEC.若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.给出以下五个结论:
如图,在矩形ABCD中,AB=2,AD=$\sqrt{3}$,在边CD上有一点E,使EB平分∠AEC.若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.给出以下五个结论:分析 由角平分线的定义和矩形的性质可证明∠AEB=∠ABE,可求得AE=AB=2,在Rt△ADE中可求得DE=1,则EC=1,又可证明△PEC∽△PBF,可求得BF=2,可判定①;在Rt△PBF中可求得PF,可判定②;在Rt△BCE中可求得BE=2,可得∠BEF=∠F,可判定③;容易计算出S矩形ABCD和S△BPF;可判定④;由AE=AB=BE可判定⑤;可得出答案.
解答 解:∵四边形ABCD为矩形,
∴AB∥CD,
∴∠CEB=∠ABE,
又∵BE平分∠AEC,
∴∠AEB=∠CEB,
∴∠AEB=∠ABE,
∴AE=AB=2,
在Rt△ADE中,AD=$\sqrt{3}$,AE=2,由勾股定理可求得DE=1,
∴CE=CD-DE=2-1=1,
∵DC∥AB,
∴△PCE∽△PBF,
∴$\frac{CE}{BF}$=$\frac{PC}{BP}$,即$\frac{1}{BF}$=$\frac{PC}{2PC}$=$\frac{1}{2}$,
∴BF=2,
∴AB=BF,
∴点B平分线段AF,
故①正确;
∵BC=AD=$\sqrt{3}$,
∴BP=$\frac{2}{3}$$\sqrt{3}$,
在Rt△BPF中,BF=2,由勾股定理可求得PF=$\sqrt{B{F}^{2}+B{P}^{2}}$=$\sqrt{4+(\frac{2}{3}\sqrt{3})^{2}}$=$\frac{4}{3}$$\sqrt{3}$,
∵DE=1,
∴PF=$\frac{4}{3}$$\sqrt{3}$DE,
故②正确;
在Rt△BCE中,EC=1,BC=$\sqrt{3}$,由勾股定理可求得BE=2,
∴BE=BF,
∴∠BEF=∠F,
又∵AB∥CD,
∴∠FEC=∠F,
∴∠BEF=∠FEC,
故③正确;
∵AB=2,AD=$\sqrt{3}$,
∴S矩形ABCD=AB•AD=2×$\sqrt{3}$=2$\sqrt{3}$,
∵BF=2,BP=$\frac{4}{3}$$\sqrt{3}$,
∴S△BPF=$\frac{1}{2}$BF•BP=$\frac{1}{2}$×2×$\frac{4}{3}$$\sqrt{3}$=$\frac{4}{3}$$\sqrt{3}$,
∴4S△BPF=$\frac{16}{3}$$\sqrt{3}$,
∴S矩形ABCD=≠4S△BPF,
故④不正确;
由上可知AB=AE=BE=2,
∴△AEB为正三角形,
故⑤正确;
综上可知正确的结论为:①②③⑤.
故答案为:①②③⑤.
点评 本题主要考查矩形的性质和相似三角形的判定和性质、等腰三角形的判定和性质、勾股定理、等边三角形的判定等知识点的综合应用.根据条件求得AE=AB,求得DE的长是解题的关键,从而可求得BF、PF、BE等线段的长容易判断②③④⑤.本题知识点较多,综合性较强,难度较大.在解题时注意勾股定理的灵活运用.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
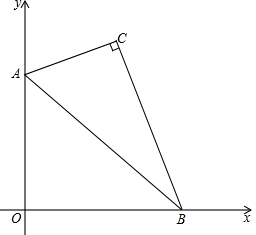 如图,将一块三内角分别为30°,60°,90°的三角板放置在直角坐标系中,三角板最长边的两个端点A、B分别在x轴、y轴的正半轴上滑动(不含坐标原点).已知:∠ACB=90°,∠CBA=30°,AB=12cm.
如图,将一块三内角分别为30°,60°,90°的三角板放置在直角坐标系中,三角板最长边的两个端点A、B分别在x轴、y轴的正半轴上滑动(不含坐标原点).已知:∠ACB=90°,∠CBA=30°,AB=12cm.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | $[{\frac{x}{10}}]$ | B. | $[{\frac{x+3}{10}}]$ | C. | $[{\frac{x+4}{10}}]$ | D. | $[{\frac{x+5}{10}}]$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com