
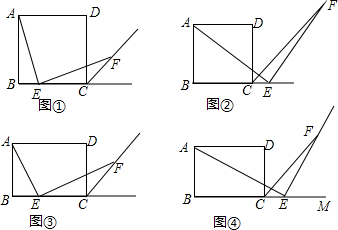
分析 (1)在AB上取点G,使得BG=BE,连接EG,根据已知条件利用ASA判定△AGE≌△ECF,因为全等三角形的对应边相等,所以AE=EF;
(2)在BA的延长线上取一点G,使AG=CE,连接EG,根据已知利用ASA判定△AGE≌△ECF,因为全等三角形的对应边相等,所以AE=EF;
(3)在AB上取点G,使得BG=BE=m,连接EG;证明△AGE∽△ECF,得出对应边成比例,即可得出结果;
(4)在BA的延长线上取点G,使得BG=BE,连接EG;同(3),证明△AGE∽△ECF,得出对应边成比例,即可得出结果.
解答 (1)证明:在AB上取点G,使得BG=BE,连接EG;如图①所示: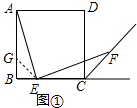
∵四边形ABCD是正方形,
∴∠B=90°,AB=BC,
∵BG=BE,
∴AG=EC,
∴△BEG为等腰直角三角形,
∴∠BGE=45°,
∴∠AGE=180°-45°=135°,
又∵CF为正方形的外角平分线,
∴∠ECF=90°+45°=135°,
∴∠AGE=∠ECF,
∵∠AEF=90°,
∴∠AEB+∠CEF=90°,
∵∠GAE+∠AEB=90°,
∴∠GAE=∠CEF,
在△AGE和△ECF中,
$\left\{\begin{array}{l}{∠GAE=∠CEF}&{\;}\\{AG=EC}&{\;}\\{∠AEG=∠ECF}&{\;}\end{array}\right.$,
∴△AGE≌△ECF(ASA),
∴AE=EF;
(2)解:AE=EF;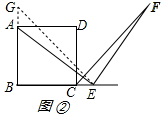
理由:在BA的延长线上取点G,使得AG=CE,连接EG.
∵四边形ABCD为正方形,AG=CE,
∴∠B=90°,BG=BE,
∴△BEG为等腰直角三角形,
∴∠G=45°,
又∵CF为正方形的外角平分线,
∴∠ECF=45°,
∴∠G=∠ECF=45°,
∵∠AEF=90°,
∴∠FEM=90°-∠AEB,
又∵∠BAE=90°-∠AEB,
∴∠FEM=∠BAE,
∴∠GAE=∠CEF,
在△AGE和△ECF中,
$\left\{\begin{array}{l}{∠G=∠CEF}&{\;}\\{AG=CE}&{\;}\\{∠GAE=∠CEF}&{\;}\end{array}\right.$,
∴△AGE≌△ECF(ASA),
∴AE=EF.
(3)证明$\frac{AE}{EF}=\frac{a-m}{b-m}$:如图③,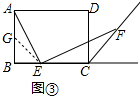 在AB上取点G,使得BG=BE=m,连接EG;
在AB上取点G,使得BG=BE=m,连接EG;
∵长方形ABCD中,∠B=90°,AB=a,BC=b,BE=m,
∴AG=a-m,EC=b-m,
∵BG=BE=m,
∴△BEG为等腰直角三角形,
∴∠AGE=180°-45°=135°,
又∵CF为正方形的外角平分线,
∴∠ECF=90°+45°=135°,
∴∠AGE=∠ECF,
∵∠AEF=90°,
∴∠GAE=90°-∠AEB=∠CEF,
∴∠GAE=∠CEF,
∴△AGE∽△ECF,
∴$\frac{AE}{EF}=\frac{AG}{EC}=\frac{a-m}{b-m}$,
故答案为:$\frac{a-m}{b-m}$;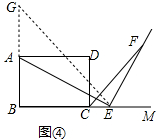 证明$\frac{AE}{EF}=\frac{m-a}{m-b}$:如图④,
证明$\frac{AE}{EF}=\frac{m-a}{m-b}$:如图④,
在BA的延长线上取点G,使得BG=BE,连接EG;
由(2)得:∠G=∠ECF=45°,∠GAE=∠CEF,
∴△AGE∽△ECF,
∴$\frac{AE}{EF}=\frac{AG}{EC}=\frac{m-a}{m-b}$,
故答案为$\frac{m-a}{m-b}$.
点评 本题是四边形综合题,考查了正方形的性质、全等三角形的判定与性质、等腰直角三角形的判定与性质、相似三角形的判定与性质等知识,本题难度较大,综合性强,特别是需要通过作辅助线证明三角形全等或相似才能得出结论.


科目:初中数学 来源: 题型:解答题
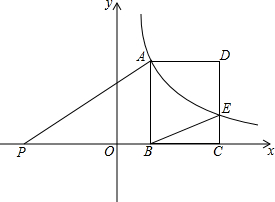 如图,矩形ABCD中,AB=3,BC=2,点A在反比例函数y=$\frac{k}{x}$(x>0),图象上点E是双曲线与CD的交点.点B,C和点P(-5,0)均在x轴上,PA∥BE.
如图,矩形ABCD中,AB=3,BC=2,点A在反比例函数y=$\frac{k}{x}$(x>0),图象上点E是双曲线与CD的交点.点B,C和点P(-5,0)均在x轴上,PA∥BE.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
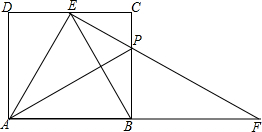 如图,在矩形ABCD中,AB=2,AD=$\sqrt{3}$,在边CD上有一点E,使EB平分∠AEC.若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.给出以下五个结论:
如图,在矩形ABCD中,AB=2,AD=$\sqrt{3}$,在边CD上有一点E,使EB平分∠AEC.若P为BC边上一点,且BP=2CP,连接EP并延长交AB的延长线于F.给出以下五个结论:查看答案和解析>>
科目:初中数学 来源: 题型:解答题
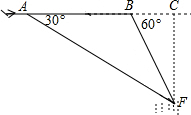 “马航事件”的发生引起了我国政府的高度重视,迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机观测得在点A俯角为30°方向的F点处有疑似飞机残骸的物体(该物体视为静止).为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F在点B俯角为60°的方向上,请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:$\sqrt{3}$≈1.7)
“马航事件”的发生引起了我国政府的高度重视,迅速派出了舰船和飞机到相关海域进行搜寻.如图,在一次空中搜寻中,水平飞行的飞机观测得在点A俯角为30°方向的F点处有疑似飞机残骸的物体(该物体视为静止).为了便于观察,飞机继续向前飞行了800米到达B点,此时测得点F在点B俯角为60°的方向上,请你计算当飞机飞临F点的正上方点C时(点A、B、C在同一直线上),竖直高度CF约为多少米?(结果保留整数,参考数值:$\sqrt{3}$≈1.7)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com