
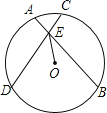
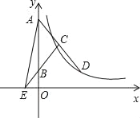
【题目】如图,⊙O的两条弦AB、CD交于点E,OE平分∠BED.
(1)求证:AB=CD;
(2)若∠BED=60°,EO=2,求DE﹣AE的值.
【答案】(1)证明见解析;(2)![]() .
.
【解析】试题(1)过点O作AB、CD的垂线,垂足为M、N,由角平分线的性质,可得OM=ON,然后由弦心距相等可得弦相等,即AB=CD;
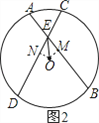
(2)由(1)可得,OM=ON,AB=CD,OM⊥AB,ON⊥CD,由垂径定理可得DN=CN=AM=BM,由HL可证Rt△EON≌Rt△EOM,继而可得NE=ME,
从而得AE=CE, DE-AE=DE-CE=DN+NE-CE=CN+NE-CE=2NE,在Rt△EON中,由∠NEO=30°,OE=2,即可求出NE.
试题解析:(1)过点O作AB、CD的垂线,垂足为M、N,如图1,

∵OE平分∠BED,且OM⊥AB,ON⊥CD,∴OM=ON,∴AB=CD;
(2)如图2所示,由(1)知,OM=ON,AB=CD,OM⊥AB,ON⊥CD,∴DN=CN=AM=BM,在Rt△EON与Rt△EOM中,∵![]() ,∴Rt△EON≌Rt△EOM(HL),∴NE=ME,∴CD﹣DN﹣NE=AB﹣BM﹣ME,即AE=CE,∴DE﹣AE=DE﹣CE=DN+NE﹣CE=CN+NE﹣CE=2NE,∵∠BED=60°,OE平分∠BED,∴∠NEO=
,∴Rt△EON≌Rt△EOM(HL),∴NE=ME,∴CD﹣DN﹣NE=AB﹣BM﹣ME,即AE=CE,∴DE﹣AE=DE﹣CE=DN+NE﹣CE=CN+NE﹣CE=2NE,∵∠BED=60°,OE平分∠BED,∴∠NEO= ![]() ∠BED=30°,∴ON=
∠BED=30°,∴ON=![]() OE=1,在Rt△EON中,由勾股定理得:NE=
OE=1,在Rt△EON中,由勾股定理得:NE=![]() =
=![]() ,∴DE﹣AE=2NE=2
,∴DE﹣AE=2NE=2![]() .
.


科目:初中数学 来源: 题型:
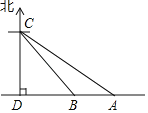
【题目】据调查,超速行驶是引发交通事故的主要原因之一.小强用所学知识对一条笔直公路上的车辆进行测速,如图所示,观测点C到公路的距离CD=200m,检测路段的起点A位于点C的南偏东60°方向上,终点B位于点C的南偏东45°方向上.一辆轿车由东向西匀速行驶,测得此车由A处行驶到B处的时间为10s.问此车是否超过了该路段16m/s的限制速度?(观测点C离地面的距离忽略不计,参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某养鸡场有2500只鸡准备对外出售.从中随机抽取了一部分鸡,根据它们的质量(单位:![]() ),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:
),绘制出如下的统计图①和图②.请根据相关信息,解答下列问题:

(Ⅰ)图①中![]() 的值为 ;
的值为 ;
(Ⅱ)求统计的这组数据的平均数、众数和中位数;
(Ⅲ) 根据样本数据,估计这2500只鸡中,质量为![]() 的约有多少只?
的约有多少只?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=-x2+bx+c的图像经过点(0,3)、(-1,0).
(1)求二次函数的表达式;
(2)在给定的平面直角坐标系中,画出这个二次函数的图像;
(3)根据图像,直接写出当x满足什么条件时,y>0.

查看答案和解析>>
科目:初中数学 来源: 题型:
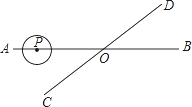
【题目】如图,直线AB、CD相交于点O,∠AOC=30°,半径为1cm的⊙P的圆心在直线AB上,且与点O的距离为6cm.如果⊙P以1cm∕s的速度,沿由A向B的方向移动,那么________秒种后⊙P与直线CD相切.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰△ABC的底边在y轴正半轴上,顶点C在第一象限,延长AC交双曲线y=![]() 于D,且CD=AC,延长CB交x轴于E,若△ABE的面积为5,则k=_____.
于D,且CD=AC,延长CB交x轴于E,若△ABE的面积为5,则k=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知:关于x的二次函数![]() 的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
的图象与x轴交于点A(1,0)和点B,与y轴交于点C(0,3),抛物线的对称轴与x轴交于点D.
(1)求二次函数的表达式;
(2)在y轴上是否存在一点P,使△PBC为等腰三角形.若存在,请求出点P的坐标;
(3)有一个点M从点A出发,以每秒1个单位的速度在AB上向点B运动,另一个点N从点D与点M同时出发,以每秒2个单位的速度在抛物线的对称轴上运动,当点M到 达点B时,点M、N同时停止运动,问点M、N运动到何处时,△MNB面积最大,试求出最大面积.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为一圆洞门.工匠在建造过程中需要一根横梁AB和两根对称的立柱CE、DF来支撑,点A、B、C、D在⊙O上,CE⊥AB于E,DF⊥AB于F,且AB=2![]() ,EF=
,EF=![]() ,
,![]() =120°.
=120°.
(1)求出圆洞门⊙O的半径;
(2)求立柱CE的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() ,
,![]() 与
与![]() 和
和![]() 分别相切于点
分别相切于点![]() 和点
和点![]() .点
.点![]() 和点
和点![]() 分别是
分别是![]() 和
和![]() 上的动点,
上的动点,![]() 沿
沿![]() 和
和![]() 平移.
平移.![]() 的半径为
的半径为![]() ,
,![]() .下列结论错误的是( )
.下列结论错误的是( )

A. ![]() B.
B. ![]() 和
和![]() 的距离为
的距离为![]()
C. 若![]() ,则
,则![]() 与
与![]() 相切 D. 若
相切 D. 若![]() 与
与![]() 相切,则
相切,则![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com