
【题目】抛物线![]() :
:![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),抛物线的顶点为
左侧),抛物线的顶点为![]() .
.
(1)抛物线![]() 的对称轴是直线________;
的对称轴是直线________;
(2)当![]() 时,求抛物线
时,求抛物线![]() 的函数表达式;
的函数表达式;
(3)在(2)的条件下,直线![]() :
:![]() 经过抛物线的顶点
经过抛物线的顶点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 有两个公共点,它们的横坐标分别记为
有两个公共点,它们的横坐标分别记为![]() ,
,![]() ,直线
,直线![]() 与直线
与直线![]() 的交点的横坐标记为
的交点的横坐标记为![]() ,若当
,若当![]() 时,总有
时,总有![]() ,请结合函数的图象,直接写出
,请结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]()
【解析】
(1)根据抛物线的函数表达式,利用二次函数的性质即可找出抛物线![]() 的对称轴;(2)根据抛物线的对称轴及
的对称轴;(2)根据抛物线的对称轴及![]() 即可得出点
即可得出点![]() 、
、![]() 的坐标,根据点
的坐标,根据点![]() 的坐标,利用待定系数法即可求出抛物线
的坐标,利用待定系数法即可求出抛物线![]() 的函数表达式;(3)利用配方法求出抛物线顶点
的函数表达式;(3)利用配方法求出抛物线顶点![]() 的坐标,依照题意画出图形,观察图形可得出
的坐标,依照题意画出图形,观察图形可得出![]() ,再利用一次函数图象上点的坐标特征可得出
,再利用一次函数图象上点的坐标特征可得出![]() ,结合
,结合![]() 的取值范围即可得出
的取值范围即可得出![]() 的取值范围.
的取值范围.
(1)∵抛物线![]() 的表达式为
的表达式为![]() ,
,
∴抛物线![]() 的对称轴为直线
的对称轴为直线![]() .
.
故答案为:![]() .
.
(2)∵抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,
,![]() ,
,
∴点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
将![]() 代入
代入![]() ,得:
,得:![]() ,
,
解得:![]() ,
,
∴抛物线![]() 的函数表达式为
的函数表达式为![]() .
.
(3)∵![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
∵直线y=n与直线![]() 的交点的横坐标记为
的交点的横坐标记为![]() ,且当
,且当![]() 时,总有
时,总有![]() ,
,
∴x2<x3<x1,
∵x3>0,
∴直线![]() 与
与![]() 轴的交点在
轴的交点在![]() 下方,
下方,
∴![]() .
.
∵直线![]() :
:![]() 经过抛物线的顶点
经过抛物线的顶点![]() ,
,
∴![]() ,
,
∴![]() .
.
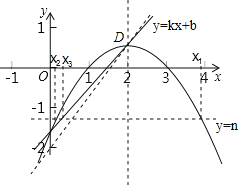


科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣2ax﹣2,与x轴交于A,B两点,与y轴交于点C,A(﹣2,0)
(1)直接写出:a=
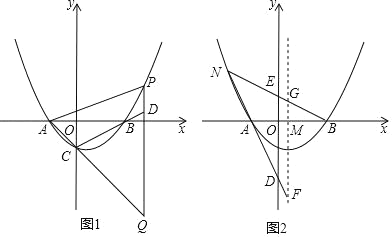
(2)如图1,点P在第一象限内抛物线上的一点,过点P作x轴的垂线交CB的延长线于点D,交AC的延长线于点Q,当△QAP与△QCD相似时,求P点的坐标;
(3)如图2,抛物线的对称轴交x轴于点M,N为第二象限内抛物线上的一点,直线NA,NB分别交y轴于D,E两点,分别交抛物线的对称轴于F,G两点.
①求tan∠FAM﹣tan∠GAM的值;
②若![]() ,求N点的坐标.
,求N点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
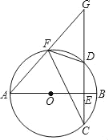
【题目】如图,已知AB是⊙O的直径,弦CD⊥AB于点E,F是弧AD上的一点,AF,CD的延长线相交于点G.
(1)若⊙O的半径为3![]() ,且∠DFC=45°,求弦CD的长.
,且∠DFC=45°,求弦CD的长.
(2)求证:∠AFC=∠DFG.
查看答案和解析>>
科目:初中数学 来源: 题型:
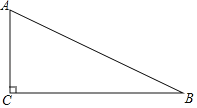
【题目】如图,在Rt△ABC中,∠C=90°,AB=8.
(1)作△ABC的内角∠CAB的平分线,与边BC交于点D(用尺规作图,保留作图痕迹,不要求写作法);
(2)若AD=BD,求CD的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料:
材料一:
早在2011年9月25日,北京故宫博物院就开始尝试网络预售门票,2011年全年网络售票仅占1.68%.2012年至2014年,全年网络售票占比都在2%左右.2015年全年网络售票占17.33%,2016年全年网络售票占比增长至41.14%.2017年8月实现网络售票占比77%.2017年10月2日,首次实现全部网上售票.与此同时,网络购票也采用了“人性化”的服务方式,为没有线上支付能力的观众提供代客下单服务.实现全网络售票措施后,在北京故宫博物院的精细化管理下,观众可以更自主地安排自己的行程计划,获得更美好的文化空间和参观体验.
材料二:
以下是某同学根据网上搜集的数据制作的2013-2017年度中国国家博物馆参观人数及年增长率统计表.
年度 | 2013 | 2014 | 2015 | 2016 | 2017 |
参观人数(人次) | 7 450 000 | 7 630 000 | 7 290 000 | 7 550 000 | 8 060 000 |
年增长率(%) | 38.7 | 2.4 | -4.5 | 3.6 | 6.8 |

他还注意到了如下的一则新闻:2018年3月8日,中国国家博物馆官方微博发文,宣布取消纸质门票,观众持身份证预约即可参观. 国博正在建设智慧国家博物馆,同时馆方工作人员担心的是:“虽然有故宫免(纸质)票的经验在前,但对于国博来说这项工作仍有新的挑战.参观故宫需要观众网上付费购买门票,他遵守预约的程度是不一样的.但(国博)免费就有可能约了不来,挤占资源,所以难度其实不一样.” 尽管如此,国博仍将积极采取技术和服务升级,希望带给观众一个更完美的体验方式.
根据以上信息解决下列问题:
(1)补全以下两个统计图;
(2)请你预估2018年中国国家博物馆的参观人数,并说明你的预估理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+2x﹣3与x轴交于A、B两点,且B(1,0)
(1)求抛物线的解析式和点A的坐标;
(2)如图1,点P是直线y=x上的动点,当直线y=x平分∠APB时,求点P的坐标;
(3)如图2,已知直线y=![]() x﹣
x﹣![]() 分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
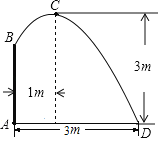
【题目】如图,在喷水池的中心A处竖直安装一个水管AB,水管的顶端安有一个喷水池,使喷出的抛物线形水柱在与池中心A的水平距离为1m处达到最高点![]() ,高度为3m,水柱落地点D离池中心A处3m,以水平方向为
,高度为3m,水柱落地点D离池中心A处3m,以水平方向为![]() 轴,建立平面直角坐标系,若选取
轴,建立平面直角坐标系,若选取![]() 点为坐标原点时的抛物线的表达式为
点为坐标原点时的抛物线的表达式为![]() ,则选取点
,则选取点![]() 为坐标原点时的抛物线表达式为______,水管
为坐标原点时的抛物线表达式为______,水管![]() 的长为______
的长为______![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的顶点A、C分别在轴的负半轴、轴的正半轴上,点B在第二象限.将矩形OABC绕点O顺时针旋转,使点B落在轴上,得到矩形ODEF,BC与OD相交于点M.若经过点M的反比例函数y=![]() (x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=
(x<0)的图象交AB于点N,的图象交AB于点N, S矩形OABC=32,tan∠DOE=![]() ,,则BN的长为______________.
,,则BN的长为______________.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com