
【题目】如图,抛物线y=ax2+2x﹣3与x轴交于A、B两点,且B(1,0)
(1)求抛物线的解析式和点A的坐标;
(2)如图1,点P是直线y=x上的动点,当直线y=x平分∠APB时,求点P的坐标;
(3)如图2,已知直线y=![]() x﹣
x﹣![]() 分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.
分别与x轴、y轴交于C、F两点,点Q是直线CF下方的抛物线上的一个动点,过点Q作y轴的平行线,交直线CF于点D,点E在线段CD的延长线上,连接QE.问:以QD为腰的等腰△QDE的面积是否存在最大值?若存在,请求出这个最大值;若不存在,请说明理由.

【答案】(1)A点坐标为(﹣3,0);(2);P点坐标为(![]() ,
, ![]() );(3)以QD为腰的等腰三角形的面积最大值为
);(3)以QD为腰的等腰三角形的面积最大值为![]() .
.
【解析】试题分析:(1)把B点的坐标代入抛物线的解析式,求出a的值即可,令y=0,解方程求得x的值,即可得点A的坐标;(2)当点P在x轴上方时,连接AP交y轴于点B′,可证△OBP≌△OB′P,可求得B′坐标,利用待定系数法可求得直线AP的解析式,联立直线y=x,可求得P点坐标;当点P在x轴下方时,同理可求得∠BPO=∠B′PO,又∠B′PO在∠APO的内部,可知此时没有满足条件的点P;(3)过Q作QH⊥DE于点H,由直线CF的解析式可求得点C、F的坐标,结合条件可求得tan∠QDH,可分别用DQ表示出QH和DH的长,分DQ=DE和DQ=QE两种情况,分别用DQ的长表示出△QDE的面积,再设出点Q的坐标,利用二次函数的性质可求得△QDE的面积的最大值.
试题解析:
(1)把B(1,0)代入y=ax2+2x﹣3,
可得a+2﹣3=0,解得a=1,
∴抛物线解析式为y=x2+2x﹣3,
令y=0,可得x2+2x﹣3=0,解得x=1或x=﹣3,
∴A点坐标为(﹣3,0);
(2)若y=x平分∠APB,则∠APO=∠BPO,
如图1,若P点在x轴上方,PA与y轴交于点B′,

由于点P在直线y=x上,可知∠POB=∠POB′=45°,
在△BPO和△B′PO中,
∠POB=∠PCB/,OP=OP,∠BPO=∠B/PO,
∴△BPO≌△B′PO(ASA),
∴BO=B′O=1,
设直线AP解析式为y=kx+b,把A、B′两点坐标代入可得
![]() ,解得
,解得 ,
,
∴直线AP解析式为y=![]() x+1,
x+1,
联立 ,解得
,解得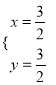 ,
,
∴P点坐标为(![]() ,
, ![]() );
);
若P点在x轴下方时,同理可得△BOP≌△B′OP,
∴∠BPO=∠B′PO,
又∠B′PO在∠APO的内部,
∴∠APO≠∠BPO,即此时没有满足条件的P点,
综上可知P点坐标为(![]() ,
, ![]() );
);
(3)如图2,作QH⊥CF,交CF于点H,

∵CF为y=![]() x﹣
x﹣![]() ,
,
∴可求得C(![]() ,0),F(0,﹣
,0),F(0,﹣![]() ),
),
∴tan∠OFC=![]() =
=![]() ,
,
∵DQ∥y轴,
∴∠QDH=∠MFD=∠OFC,
∴tan∠HDQ=![]() ,
,
不妨设DQ=t,DH=![]() t,HQ=
t,HQ=![]() t,
t,
∵△QDE是以DQ为腰的等腰三角形,
∴若DQ=DE,则S△DEQ=![]() DEHQ=
DEHQ=![]() ×
×![]() t×t=
t×t=![]() t2,
t2,
若DQ=QE,则S△DEQ=![]() DEHQ=
DEHQ=![]() ×2DHHQ=
×2DHHQ=![]() ×
×![]() t×
t×![]() t=
t=![]() t2,
t2,
∵![]() t2<
t2<![]() t2,
t2,
∴当DQ=QE时△DEQ的面积比DQ=DE时大.
设Q点坐标为(x,x2+2x﹣3),则D(x, ![]() x﹣
x﹣![]() ),
),
∵Q点在直线CF的下方,
∴DQ=t=![]() x﹣
x﹣![]() ﹣(x2+2x﹣3)=﹣x2﹣
﹣(x2+2x﹣3)=﹣x2﹣![]() x+
x+![]() ,
,
当x=﹣![]() 时,tmax=3,
时,tmax=3,
∴(S△DEQ)max=![]() t2=
t2=![]() ,
,
即以QD为腰的等腰三角形的面积最大值为![]() .
.


 小学期末标准试卷系列答案
小学期末标准试卷系列答案科目:初中数学 来源: 题型:
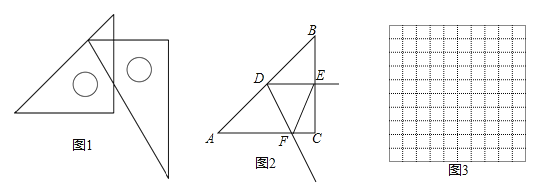
【题目】在数学活动课上,老师提出了一个问题:把一副三角尺如图摆放,直角三角尺的两条直角边分别垂直或平行,60°角的顶点在另一个三角尺的斜边上移动,在这个运动过程中,有哪些变量,能研究它们之间的关系吗?
小林选择了其中一对变量,根据学习函数的经验,对它们之间的关系进行了探究.
下面是小林的探究过程,请补充完整:
(1)画出几何图形,明确条件和探究对象;
如图2,在Rt△ABC中,∠C=90°,AC=BC=6cm,D是线段AB上一动点,射线DE⊥BC于点E,∠EDF=60°,射线DF与射线AC交于点F.设B,E两点间的距离为xcm,E,F两点间的距离为ycm.
(2)通过取点、画图、测量,得到了x与y的几组值,如下表:
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 6.9 | 5.3 | 4.0 | 3.3 | 4.5 | 6 |
(说明:补全表格时相关数据保留一位小数)
(3)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(4)结合画出的函数图象,解决问题:当△DEF为等边三角形时,BE的长度约为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
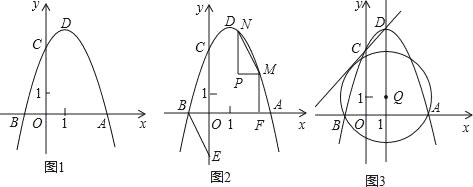
【题目】如图1,二次函数y=ax2﹣2ax﹣3a(a<0)的图象与x轴交于A、B两点(点A在点B的右侧),与y轴的正半轴交于点C,顶点为D.
(1)求顶点D的坐标(用含a的代数式表示);
(2)若以AD为直径的圆经过点C.
①求抛物线的函数关系式;
②如图2,点E是y轴负半轴上一点,连接BE,将△OBE绕平面内某一点旋转180°,得到△PMN(点P、M、N分别和点O、B、E对应),并且点M、N都在抛物线上,作MF⊥x轴于点F,若线段MF:BF=1:2,求点M、N的坐标;
③点Q在抛物线的对称轴上,以Q为圆心的圆过A、B两点,并且和直线CD相切,如图3,求点Q的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1所示,甲、乙两车沿直路同向行驶,车速分别为20 m/s和v(m/s),起初甲车在乙 车前a (m)处,两车同时出发,当乙车追上甲车时,两车都停止行驶.设x(s)后两车相距y (m),y与x的函数关系如图2所示.有以下结论:
①图1中a的值为500;
②乙车的速度为35 m/s;
③图1中线段EF应表示为![]() ;
;
④图2中函数图象与x轴交点的横坐标为100.
其中所有的正确结论是( )
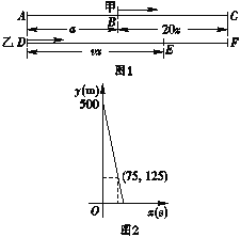
A. ①④ B. ②③
C. ①②④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线![]() :
:![]() 与
与![]() 轴交于
轴交于![]() ,
,![]() 两点(点
两点(点![]() 在点
在点![]() 左侧),抛物线的顶点为
左侧),抛物线的顶点为![]() .
.
(1)抛物线![]() 的对称轴是直线________;
的对称轴是直线________;
(2)当![]() 时,求抛物线
时,求抛物线![]() 的函数表达式;
的函数表达式;
(3)在(2)的条件下,直线![]() :
:![]() 经过抛物线的顶点
经过抛物线的顶点![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 有两个公共点,它们的横坐标分别记为
有两个公共点,它们的横坐标分别记为![]() ,
,![]() ,直线
,直线![]() 与直线
与直线![]() 的交点的横坐标记为
的交点的横坐标记为![]() ,若当
,若当![]() 时,总有
时,总有![]() ,请结合函数的图象,直接写出
,请结合函数的图象,直接写出![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面的两个统计图是中国互联网信息中心发布的第43次《中国互联网络发展状况统计报告》的内容,上图为网民规模和互联网普及率,下图为手机网民规模及其占网民比例.根据统计图提供的信息,下面推断不合理的是( )

A.2008~2018年,网民规模和手机网民规模都在逐年上升
B.相比其它年份,2009年手机网民占整体网民的增长比例最大
C.2008年手机上网人数只占全体国民的![]() 左右
左右
D.预计2019年网民规模不会低于![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
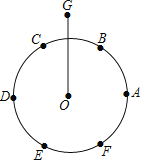
【题目】尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:
①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;
②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;
③连结OG.
问:OG的长是多少?
大臣给出的正确答案应是( )
A. ![]() r B. (1+
r B. (1+![]() )r C. (1+
)r C. (1+![]() )r D.
)r D. ![]() r
r
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两人约好步行沿同一路线同一方向在某景点集合,已知甲乙二人相距660米,二人同时出发,走了24分钟时,由于乙距离景点近,先到达等候甲,甲共走了30分钟也到达了景点与乙相遇.在整个行走过程中,甲、乙两人均保持各自的速度匀速行走,甲、乙两人相距的路程![]() (米)与甲出发的时间
(米)与甲出发的时间![]() (分钟)之间的关系如图所示,下列说法错误的是( )
(分钟)之间的关系如图所示,下列说法错误的是( )

A.甲的速度是70米/分B.乙的速度是60米/分
C.甲距离景点2100米D.乙距离景点420米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市东坡实验中学准备开展“阳光体育活动”,决定开设足球、篮球、乒乓球、羽毛球、排球等球类活动,为了了解学生对这五项活动的喜爱情况,随机调查了![]() 名学生(每名学生必选且只能选择这五项活动中的一种).
名学生(每名学生必选且只能选择这五项活动中的一种).
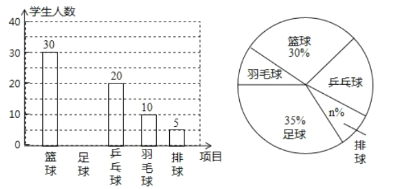
根据以上统计图提供的信息,请解答下列问题:
(1)![]() ,
,![]() .
.
(2)补全上图中的条形统计图.
(3)若全校共有![]() 名学生,请求出该校约有多少名学生喜爱打乒乓球.
名学生,请求出该校约有多少名学生喜爱打乒乓球.
(4)在抽查的![]() 名学生中,有小薇、小燕、小红、小梅等
名学生中,有小薇、小燕、小红、小梅等![]() 名学生喜欢羽毛球活动,学校打算从小薇、小燕、小红、小梅这
名学生喜欢羽毛球活动,学校打算从小薇、小燕、小红、小梅这![]() 名女生中,选取
名女生中,选取![]() 名参加全市中学生女子羽毛球比赛,请用列表法或画树状图法,求同时选中小红、小燕的概率.(解答过程中,可将小薇、小燕、小红、小梅分别用字母
名参加全市中学生女子羽毛球比赛,请用列表法或画树状图法,求同时选中小红、小燕的概率.(解答过程中,可将小薇、小燕、小红、小梅分别用字母![]() 、
、![]() 、
、![]() 、
、![]() 代表)
代表)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com