
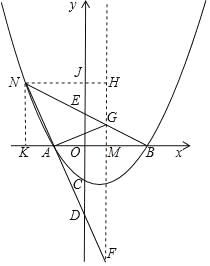
ЁОЬтФПЁПвбжЊХзЮяЯпyЃНax2Љ2axЉ2ЃЌгыxжсНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкЕуCЃЌAЃЈЉ2ЃЌ0ЃЉ
ЃЈ1ЃЉжБНгаДГіЃКaЃНЁЁ ЁЁ
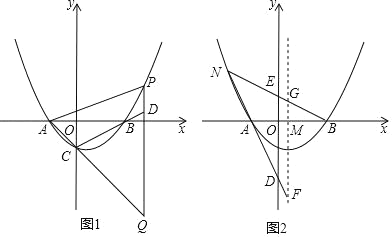
ЃЈ2ЃЉШчЭМ1ЃЌЕуPдкЕквЛЯѓЯоФкХзЮяЯпЩЯЕФвЛЕуЃЌЙ§ЕуPзїxжсЕФДЙЯпНЛCBЕФбгГЄЯпгкЕуDЃЌНЛACЕФбгГЄЯпгкЕуQЃЌЕБЁїQAPгыЁїQCDЯрЫЦЪБЃЌЧѓPЕуЕФзјБъЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌХзЮяЯпЕФЖдГЦжсНЛxжсгкЕуMЃЌNЮЊЕкЖўЯѓЯоФкХзЮяЯпЩЯЕФвЛЕуЃЌжБЯпNAЃЌNBЗжБ№НЛyжсгкDЃЌEСНЕуЃЌЗжБ№НЛХзЮяЯпЕФЖдГЦжсгкFЃЌGСНЕуЃЎ
ЂйЧѓtanЁЯFAMЉtanЁЯGAMЕФжЕЃЛ
ЂкШє![]() ЃЌЧѓNЕуЕФзјБъЃЎ
ЃЌЧѓNЕуЕФзјБъЃЎ
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЕуPЕФзјБъЮЊЃЈ6ЃЌ4ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЛ
ЃЉЃЛ
ЃЈ3ЃЉЂйtanЁЯFAMЉtanЁЯGAMЃН![]() ЃЛЂкЕуNЕФзјБъЮЊЃЈЉ4ЃЌ4ЃЉЃЎ
ЃЛЂкЕуNЕФзјБъЮЊЃЈЉ4ЃЌ4ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉНЋЕуAДњШыХзЮяЯпМДПЩЃЎ
ЃЈ2ЃЉЯрЫЦЗжСНжжЧщПіЃЌвЛжжЪЧAPЁЮCDЃЌИљОнСНжБЯпЦНааkЯрЕШЃЌдйДњШыЕуAОЭПЩвдЧѓГіДЫЪБжБЯпAPЕФНтЮіЪНЃЌКЭХзЮяЯпСЊСЂОЭПЩвдЧѓГіЕуPЕФзјБъЃЛСэвЛжжИљОнЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§ЃЌСаЗНГЬЧѓНтМДПЩЃЎ
ЃЈ3ЃЉЂйЩшЕуNЕФзјБъЃЌБэЪОЯпЖЮГЄЖШЃЌСаБШжЕЫуГіЪ§жЕМДПЩЃЎЂкзЊЛЛЬтИЩжаЕФБШжЕЃЌАбаБЯпЕФБШжЕзЊЛЛЮЊЫЎЦНЯпЕФБШжЕЃЌБэЪОЯпЖЮГЄЖШЃЌСаЪНЧѓНтМДПЩЃЎ
НтЃКЃЈ1ЃЉНЋAЃЈЉ2ЃЌ0ЃЉДњШыХзЮяЯпжаЃЌЕУ
0ЃН4a+4aЉ2ЃЌНтЕУ![]() ЃЎ
ЃЎ
ЙЪД№АИЮЊ![]() ЃЎ
ЃЎ
ЃЈ2ЃЉХзЮяЯпЕФНтЮіЪНЮЊ![]() ЃЌ
ЃЌ
СюyЃН0ЃЌНтЕУx1ЃНЉ2ЃЌx2ЃН4ЃЌ
ЁрBЃЈ4ЃЌ0ЃЉЃЌ
СюxЃН0ЃЌyЃНЉ2ЃЌ
ЁрCЃЈ0ЃЌЉ2ЃЉЃЌ
ЩшжБЯпACЕФНтЮіЪНЮЊyЃНkx+bЃЌДњШыЕуAЁЂCЃЌЕУЃК![]()
НтЕУ![]()
ЁрyЃНЉxЉ2ЃЌ
ЩшжБЯпBCЕФНтЮіЪНЮЊyЃНk1 x+b1ЃЌДњШыЕуЕуBЁЂCЃЌЕУЃК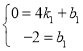
НтЕУ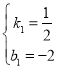
ЁрyЃН![]() xЉ2ЃЌ
xЉ2ЃЌ
ЩшЕуPЕФКсзјБъЮЊmЃЌдђзнзјБъЮЊ![]() ЃЌ
ЃЌ
дђЕуDЃЈmЃЌ ![]() mЉ2ЃЉЃЌQЃЈmЃЌЉmЉ2ЃЉЃЌ
mЉ2ЃЉЃЌQЃЈmЃЌЉmЉ2ЃЉЃЌ
PQЃН![]() ЃЌ
ЃЌ
DQЃН![]() ЃЌ
ЃЌ
AQЃН![]() ЃЌ
ЃЌ
CQЃН![]() ЃЌ
ЃЌ
ЂйЕБAPЁЮCDЪБЃЌЁїAPQЁзЁїCDQЃЌ
ЩшжБЯпAPЕФНтЮіЪНЮЊyЃН![]() x+b3ЃЌ
x+b3ЃЌ
ДњШыЕуAЃЌ0ЃН![]() ЁСЃЈЉ2ЃЉ+b3ЃЌНтЕУb3ЃН1ЃЌ
ЁСЃЈЉ2ЃЉ+b3ЃЌНтЕУb3ЃН1ЃЌ
ЁрyЃН![]() x+1ЃЌ
x+1ЃЌ
Сю![]() x+1ЃН
x+1ЃН![]() x2Љ
x2Љ![]() Љ2ЃЌ
Љ2ЃЌ
НтЕУx1ЃНЉ2ЃЌx2ЃН6ЃЌ
ЕБxЃН6ЪБЃЌyЃН4ЃЌ
ЁрPЃЈ6ЃЌ4ЃЉЃЎ
ЂкЕБЁЯAPQЃНЁЯQCDЪБЃЌЁїAPQЁзЁїDCQЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёр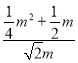 ЃН
ЃН
НтЕУm1ЃНЉ2ЃЈЩсЃЉЃЌm2ЃН![]() ЃЌ
ЃЌ
ЕБxЃН![]() ЪБЃЌyЃН
ЪБЃЌyЃН![]() ЃЌ
ЃЌ
ЁрPЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
злЩЯЫљЪіЃЌЕуPЕФзјБъЮЊЃЈ6ЃЌ4ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЃЎ
ЃЉЃЎ
ЃЈ3ЃЉЂйЙ§ЕуNзїNKДЙжБxжсгкЕуKЃЌ
ЩшЕуNЕФзјБъЮЊЃЈnЃЌ![]() n2Љ
n2Љ![]() nЉ2ЃЉЃЌ
nЉ2ЃЉЃЌ
дђNKЃН![]() n2Љ
n2Љ![]() nЉ2ЃЌAKЃНЉ2ЉnЃЌBKЃН4ЉnЃЌ
nЉ2ЃЌAKЃНЉ2ЉnЃЌBKЃН4ЉnЃЌ
tanЁЯFAMЃНtanЁЯNAK=![]() ЃН
ЃН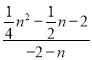 ЃЌ
ЃЌ
tanЁЯGAMЃНtanЁЯGBK=![]() ЃН
ЃН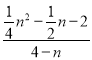 ЃЌ
ЃЌ
ЁрtanЁЯFAMЉtanЁЯGAMЃН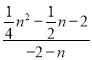 -
-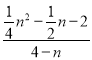 =
=![]() ЃЎ
ЃЎ
ЂкЁп![]() ЃЌЁїNEDЁзЁїNGFЃЌ
ЃЌЁїNEDЁзЁїNGFЃЌ
Ёр![]() ЃЌ
ЃЌ
Й§ЕуNЯђХзЮяЯпЕФЖдГЦжсзїДЙЯпЃЌЗжБ№НЛyжсКЭЖдГЦжсгкЕуJЁЂHЃЌ
ЁрЁїNJEЁзЁїNHGЃЌ
Ёр![]() ЃЌ
ЃЌ
NJЃНЉnЃЌNHЃН1ЉnЃЌ
Ёр4ЃЈ1ЉnЃЉЃНЉ5nЃЌ
НтЕУnЃНЉ4ЃЌ
ЕБxЃНЉ4ЪБЃЌyЃН4ЃЌ
ЁрЕуNЕФзјБъЮЊЃЈЉ4ЃЌ4ЃЉЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
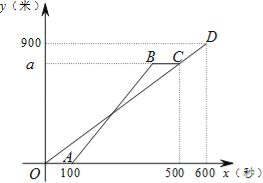
ЁОЬтФПЁПМзЁЂввСНШЫДгЫГвхЩйФъЙЌГіЗЂЃЌбиЯрЭЌЕФЯпТЗХмЯђЫГвхЙЋдАЃЌМзЯШХмвЛЖЮТЗГЬКѓЃЌввПЊЪМГіЗЂЃЌЕБввГЌЙ§Мз150УзЪБЃЌввЭЃдкДЫЕиЕШКђМзЃЌСНШЫЯргіКѓЃЌввКЭМзвЛЦ№вдМздРДЕФЫйЖШХмЯђЫГвхЙЋдАЃЌШчЭМЪЧМзЁЂввСНШЫдкХмВНЕФШЋЙ§ГЬжаОЙ§ЕФТЗГЬyЃЈУзЃЉгыМзГіЗЂЕФЪБМфxЃЈУыЃЉЕФКЏЪ§ЭМЯѓЃЌЧыИљОнЬтвтНтД№ЯТСаЮЪЬтЃЎ
ЃЈ1ЃЉдкХмВНЕФШЋЙ§ГЬжаЃЌМзЙВХмСЫ УзЃЌМзЕФЫйЖШЮЊ Уз/УыЃЛ
ЃЈ2ЃЉЧѓввХмВНЕФЫйЖШМАввдкЭОжаЕШКђМзЕФЪБМфЃЛ
ЃЈ3ЃЉЧѓввГіЗЂЖрГЄЪБМфЕквЛДЮгыМзЯргіЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЮЊЕШБпШ§НЧаЮЃЌЕу
ЮЊЕШБпШ§НЧаЮЃЌЕу![]() ЪЧЯпЖЮ
ЪЧЯпЖЮ![]() ЩЯвЛЖЏЕуЃЈЕу
ЩЯвЛЖЏЕуЃЈЕу![]() ВЛгы
ВЛгы![]() ЃЌ
ЃЌ![]() жиКЯЃЉЃЌСЌНг
жиКЯЃЉЃЌСЌНг![]() ЃЌЙ§Еу
ЃЌЙ§Еу![]() зїжБЯп
зїжБЯп![]() ЕФДЙЯпЖЮЃЌДЙзуЮЊЕу
ЕФДЙЯпЖЮЃЌДЙзуЮЊЕу![]() ЃЌНЋЯпЖЮ
ЃЌНЋЯпЖЮ![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЕУЕНЯпЖЮ
ЕУЕНЯпЖЮ![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓжЄЃК![]() ЃЛ
ЃЛ
ЃЈ2ЃЉбгГЄ![]() НЛ
НЛ![]() гкЕу
гкЕу![]() ЃЌЧѓжЄЃК
ЃЌЧѓжЄЃК![]() ЮЊ
ЮЊ![]() ЕФжаЕуЃЛ
ЕФжаЕуЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШє![]() ЕФБпГЄЮЊ1ЃЌжБНгаДГі
ЕФБпГЄЮЊ1ЃЌжБНгаДГі![]() ЕФзюДѓжЕЃЎ
ЕФзюДѓжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
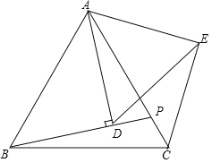
ЁОЬтФПЁПШчЭМЃЌдкABCDжаЃЌAEЁЭBCгкЕуEЃЌбгГЄBCжСЕуFЪЙCFЃНBEЃЌСЌНсAFЃЌDEЃЌDF.
(1)ЧѓжЄЃКЫФБпаЮAEFDЪЧОиаЮЃЛ
(2)ШєABЃН6ЃЌDEЃН8ЃЌBFЃН10ЃЌЧѓAEЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТСаВФСЯЃК
РїКІСЫЃЌЮвЕФЙњЃЁ
НќФъРДЃЌжаЙњЖдЭтПЊЗХЕФВНЗЅМгПьЃЌгыЪРНчОМУЕФШкКЯЖШШевцЬсИпЃЌжаЙњОМУЮШЖЈдіГЄЪЧЪРНчОМУИДЫеЕФжївЊЖЏСІЃЎЁАЪЎЖўЮхЁБЪБЦкЃЌАДее2010ФъУРдЊВЛБфМлМЦЫуЃЌжаЙњЖдЪРНчОМУдіГЄЕФФъОљЙБЯзТЪДяЕН30.5%ЃЌдООгШЋЧђЕквЛЃЌгыЁАЪЎЮхЁБКЭЁАЪЎвЛЮхЁБЪБЦк14.2%ЕФФъОљЙБЯзТЪЯрБШЃЌЬсИп16.3ИіАйЗжЕуЃЌЭЌЦкУРЙњКЭХЗдЊЧјЗжБ№ЮЊ17.8%КЭ4.4%ЃЎЗжФъЖШРДПДЃЌ2011ЁЂ2012ЁЂ2013ЁЂ2014ЁЂ2015ФъЃЌжаЙњЖдЪРНчОМУдіГЄЕФЙБЯзТЪЗжБ№ЮЊ28.6%ЁЂ31.7%ЁЂ32.5%ЁЂ29.7%ЁЂ30.0%ЃЌЖјУРЙњЗжБ№ЮЊ11.8%ЁЂ20.4%ЁЂ15.2%ЁЂ19.6%ЁЂ21.9%ЃЎ
2016ФъЃЌжаЙњЖдЪРНчОМУдіГЄЕФЙБЯзТЪШдОгЪзЮЛЃЌдЄМЦШЋФъОМУдіЫйЮЊ6.7%зѓгвЃЌЖјЪРНчвјаадЄВтШЋЧђОМУдіЫйЮЊ2.4%зѓгвЃЎАД2010ФъУРдЊВЛБфМлМЦЫуЃЌ2016ФъжаЙњЖдЪРНчОМУдіГЄЕФЙБЯзТЪШдШЛДяЕН33.2%ЃЎШчЙћАДее2015ФъМлИёМЦЫуЃЌдђжаЙњЖдЪРНчОМУдіГЄЕФЙБЯзТЪЛсИќИпвЛЕуЃЌИљОнгаЙиЙњМЪзщжЏдЄВтЃЌ2016ФъжаЙњЁЂУРЙњЁЂШеБООМУдіЫйЗжБ№ЮЊ6.7%ЁЂ1.6%ЁЂ0.6%ЃЎ
ИљОнвдЩЯВФСЯНтД№ЯТСаЮЪЬтЃК
ЃЈ1ЃЉбЁдёКЯЪЪЕФЭГМЦЭМЛђЭГМЦБэНЋ2013ФъжС2015ФъжаЙњКЭУРЙњЖдЪРНчОМУдіГЄЕФЙБЯзТЪБэЪОГіРДЃЛ
ЃЈ2ЃЉИљОнЬтжаЯрЙиаХЯЂЃЌ2016ФъжаЙњОМУдіЫйДѓдМЪЧШЋЧђОМУдіЫйЕФ БЖЃЈБЃСє1ЮЛаЁЪ§ЃЉЃЛ
ЃЈ3ЃЉИљОнЬтжаЯрЙиаХЯЂЃЌдЄЙР2017ФъжаЙњЖдЪРНчОМУдіГЄЕФЙБЯзТЪдМЮЊ ЃЌФуЕФдЄЙРРэгЩЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЪ§бЇЛюЖЏПЮЩЯЃЌРЯЪІЬсГіСЫвЛИіЮЪЬтЃКАбвЛИБШ§НЧГпШчЭМАкЗХЃЌжБНЧШ§НЧГпЕФСНЬѕжБНЧБпЗжБ№ДЙжБЛђЦНааЃЌ60ЁуНЧЕФЖЅЕудкСэвЛИіШ§НЧГпЕФаББпЩЯвЦЖЏЃЌдкетИідЫЖЏЙ§ГЬжаЃЌгаФФаЉБфСПЃЌФмбаОПЫќУЧжЎМфЕФЙиЯЕТ№ЃП
аЁСжбЁдёСЫЦфжавЛЖдБфСПЃЌИљОнбЇЯАКЏЪ§ЕФОбщЃЌЖдЫќУЧжЎМфЕФЙиЯЕНјааСЫЬНОПЃЎ
ЯТУцЪЧаЁСжЕФЬНОПЙ§ГЬЃЌЧыВЙГфЭъећЃК
ЃЈ1ЃЉЛГіМИКЮЭМаЮЃЌУїШЗЬѕМўКЭЬНОПЖдЯѓЃЛ
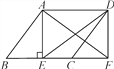
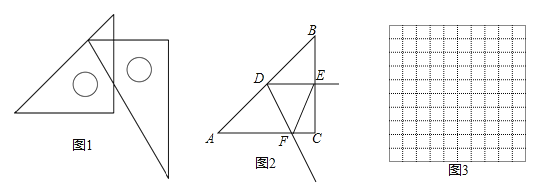
ШчЭМ2ЃЌдкRtЁїABCжаЃЌЁЯC=90ЁуЃЌAC=BC=6cmЃЌDЪЧЯпЖЮABЩЯвЛЖЏЕуЃЌЩфЯпDEЁЭBCгкЕуEЃЌЁЯEDF=60ЁуЃЌЩфЯпDFгыЩфЯпACНЛгкЕуFЃЎЩшBЃЌEСНЕуМфЕФОрРыЮЊxcmЃЌEЃЌFСНЕуМфЕФОрРыЮЊycmЃЎ
ЃЈ2ЃЉЭЈЙ§ШЁЕуЁЂЛЭМЁЂВтСПЃЌЕУЕНСЫxгыyЕФМИзщжЕЃЌШчЯТБэЃК
x/cm | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
y/cm | 6.9 | 5.3 | 4.0 | 3.3 | 4.5 | 6 |
ЃЈЫЕУїЃКВЙШЋБэИёЪБЯрЙиЪ§ОнБЃСєвЛЮЛаЁЪ§ЃЉ
ЃЈ3ЃЉНЈСЂЦНУцжБНЧзјБъЯЕЃЌУшГівдВЙШЋКѓЕФБэжаИїЖдЖдгІжЕЮЊзјБъЕФЕуЃЌЛГіИУКЏЪ§ЕФЭМЯѓЃЛ
ЃЈ4ЃЉНсКЯЛГіЕФКЏЪ§ЭМЯѓЃЌНтОіЮЪЬтЃКЕБЁїDEFЮЊЕШБпШ§НЧаЮЪБЃЌBEЕФГЄЖШдМЮЊ cmЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїЦяздааГЕЩЯбЇЃЌПЊЪМвде§ГЃЫйЖШдШЫйааЪЛЃЌЕЋаажСжаЭОЪБЃЌздааГЕГіСЫЙЪеЯЃЌжЛКУЭЃЯТРДаоГЕЃЌГЕаоКУКѓЃЌвђХТЕЂЮѓЩЯПЮЃЌЫћБШаоГЕЧАМгПьСЫЫйЖШМЬајдШЫйааЪЛЃЌЯТУцЪЧааЪЛТЗГЬsЃЈmЃЉЙигкЪБМфtЃЈminЃЉЕФКЏЪ§ЭМЯѓЃЌФЧУДЗћКЯаЁУїааЪЛЧщПіЕФДѓжТЭМЯѓЪЧЃЈЃЉ
A. B.
B. C.
C. D.
D.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
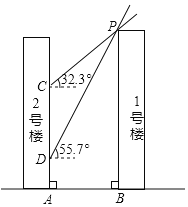
ЁОЬтФПЁПШчЭМЃЌ1КХТЅдк2КХТЅЕФФЯВрЃЌТЅМфОрЮЊABЃЎЖЌжСШее§ЮчЃЌЬЋбєЙтЯпгыЫЎЦНУцЫљГЩЕФНЧЮЊ32.3ЁуЃЌ1КХТЅдк2КХТЅЧНУцЩЯЕФгАИпЮЊCAЃЛДКЗжШее§ЮчЃЌЬЋбєЙтЯпгыЫЎЦНУцЫљГЩЕФНЧЮЊ55.7ЁуЃЌ1КХТЅдк2КХТЅЧНУцЩЯЕФгАИпЮЊDAЃЎвбжЊCD=35mЃЎЧыЧѓГіСНТЅжЎМфЕФОрРыABЕФГЄЖШЃЈНсЙћБЃСєећЪ§ЃЉ
ЃЈВЮПМЪ§ОнЃКsin32.3ЁуЁж0.53ЃЌcos32.3ЁуЁж0.85ЃЌtan32.3ЁуЁж0.63ЃЌsin55.7ЁуЁж0.83ЃЌcos55.7ЁуЁж0.56ЃЌtan55.7ЁуЁж1.47ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПХзЮяЯп![]() ЃК
ЃК![]() гы
гы![]() жсНЛгк
жсНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЈЕу
СНЕуЃЈЕу![]() дкЕу
дкЕу![]() зѓВрЃЉЃЌХзЮяЯпЕФЖЅЕуЮЊ
зѓВрЃЉЃЌХзЮяЯпЕФЖЅЕуЮЊ![]() ЃЎ
ЃЎ
ЃЈ1ЃЉХзЮяЯп![]() ЕФЖдГЦжсЪЧжБЯп________ЃЛ
ЕФЖдГЦжсЪЧжБЯп________ЃЛ
ЃЈ2ЃЉЕБ![]() ЪБЃЌЧѓХзЮяЯп
ЪБЃЌЧѓХзЮяЯп![]() ЕФКЏЪ§БэДяЪНЃЛ
ЕФКЏЪ§БэДяЪНЃЛ
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌжБЯп![]() ЃК
ЃК![]() ОЙ§ХзЮяЯпЕФЖЅЕу
ОЙ§ХзЮяЯпЕФЖЅЕу![]() ЃЌжБЯп
ЃЌжБЯп![]() гыХзЮяЯп
гыХзЮяЯп![]() гаСНИіЙЋЙВЕуЃЌЫќУЧЕФКсзјБъЗжБ№МЧЮЊ
гаСНИіЙЋЙВЕуЃЌЫќУЧЕФКсзјБъЗжБ№МЧЮЊ![]() ЃЌ
ЃЌ![]() ЃЌжБЯп
ЃЌжБЯп![]() гыжБЯп
гыжБЯп![]() ЕФНЛЕуЕФКсзјБъМЧЮЊ
ЕФНЛЕуЕФКсзјБъМЧЮЊ![]() ЃЌШєЕБ
ЃЌШєЕБ![]() ЪБЃЌзмга
ЪБЃЌзмга![]() ЃЌЧыНсКЯКЏЪ§ЕФЭМЯѓЃЌжБНгаДГі
ЃЌЧыНсКЯКЏЪ§ЕФЭМЯѓЃЌжБНгаДГі![]() ЕФШЁжЕЗЖЮЇЃЎ
ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com