
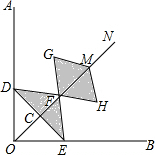
 如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )| A. | y=$\frac{{\sqrt{3}}}{2}{x^2}$ | B. | y=$\sqrt{3}{x^2}$ | C. | y=2$\sqrt{3}{x^2}$ | D. | y=3$\sqrt{3}{x^2}$ |
分析 由在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,可得△OCD与△OCE是等腰直角三角形,即可得OC垂直平分DE,求得DE=2x,再由∠DFE=∠GFH=120°,可求得C与DF,EF的长,继而求得△DF的面积,再由菱形FGMH中,FG=FE,得到△FGM是等边三角形,即可求得其面积,继而求得答案.
解答 解:∵ON是Rt∠AOB的平分线,
∴∠DOC=∠EOC=45°,
∵DE⊥OC,
∴∠ODC=∠OEC=45°,
∴CD=CE=OC=x,
∴DF=EF,DE=CD+CE=2x,
∵∠DFE=∠GFH=120°,
∴∠CEF=30°,
∴CF=CE•tan30°=$\frac{\sqrt{3}}{3}$x,
∴EF=2CF=$\frac{2\sqrt{3}}{3}$x,
∴S△DEF=$\frac{1}{2}$DE•CF=$\frac{\sqrt{3}}{3}$x2,
∵四边形FGMH是菱形,
∴FG=MG=FE=$\frac{2\sqrt{3}}{3}$x,
∵∠G=180°-∠GFH=60°,
∴△FMG是等边三角形,
∴S△FGH=$\frac{\sqrt{3}}{3}$x2,
∴S菱形FGMH=$\frac{2\sqrt{3}}{3}$x2,
∴S阴影=S△DEF+S菱形FGMH=$\sqrt{3}$x2.
故选B.
点评 此题考查了菱形的性质、等腰直角三角形的性质、等边三角形的判定与性质以及三角函数等知识.注意证得△OCD与△OCE是等腰直角三角形,△FGM是等边三角形是关键.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案科目:初中数学 来源: 题型:填空题
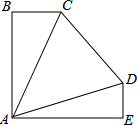 将三个三角形(△ABC、△ACD、△ADE)拼接在一起恰巧组成∠BAE=90°,AB=AE,已知BC=3,DE=2,∠B=∠E=90°,∠CAD=45°,则CD长为5.
将三个三角形(△ABC、△ACD、△ADE)拼接在一起恰巧组成∠BAE=90°,AB=AE,已知BC=3,DE=2,∠B=∠E=90°,∠CAD=45°,则CD长为5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
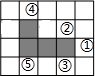 如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
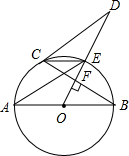 如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC.
如图,AB是⊙O的直径,OD⊥弦BC于点F,交⊙O于点E,连结CE、AE、CD,若∠AEC=∠ODC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 以正方形ABCD两条对角线的交点O为坐标原点,建立如图所示的平面直角坐标系,双曲线y=$\frac{3}{x}$经过点D,则正方形ABCD的面积是( )
以正方形ABCD两条对角线的交点O为坐标原点,建立如图所示的平面直角坐标系,双曲线y=$\frac{3}{x}$经过点D,则正方形ABCD的面积是( )| A. | 10 | B. | 11 | C. | 12 | D. | 13 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com