
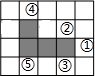
 如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案科目:初中数学 来源: 题型:选择题
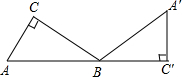 在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )
在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )| A. | $\frac{5}{2}π$ | B. | $\frac{{5\sqrt{3}}}{3}π$ | C. | $\frac{{4\sqrt{3}}}{3}π$ | D. | 2π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
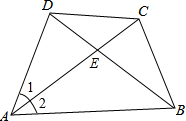 四边形ABCD中,AC为AB、AD的比例中项,且AC平分∠DAB,求证:$\frac{BE}{DE}$=$\frac{B{C}^{2}}{C{D}^{2}}$.
四边形ABCD中,AC为AB、AD的比例中项,且AC平分∠DAB,求证:$\frac{BE}{DE}$=$\frac{B{C}^{2}}{C{D}^{2}}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
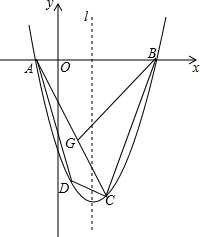 如图,已知二次函数的图象M经过A(-1,0),B(4,0),C(2,-6)三点.
如图,已知二次函数的图象M经过A(-1,0),B(4,0),C(2,-6)三点.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
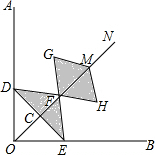 如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )
如图,在Rt∠AOB的平分线ON上依次取点C,F,M,过点C作DE⊥OC,分别交OA,OB于点D,E,以FM为对角线作菱形FGMH.已知∠DFE=∠GFH=120°,FG=FE,设OC=x,图中阴影部分面积为y,则y与x之间的函数关系式是( )| A. | y=$\frac{{\sqrt{3}}}{2}{x^2}$ | B. | y=$\sqrt{3}{x^2}$ | C. | y=2$\sqrt{3}{x^2}$ | D. | y=3$\sqrt{3}{x^2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com