
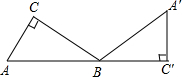
 在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )
在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )| A. | $\frac{5}{2}π$ | B. | $\frac{{5\sqrt{3}}}{3}π$ | C. | $\frac{{4\sqrt{3}}}{3}π$ | D. | 2π |
分析 根据直角三角形两锐角互余求出∠ABC=30°,根据直角三角形30°角所对的直角边等于斜边的一半可得AB=2AC,再根据旋转的性质可得∠A′BC′=∠ABC,然后求出旋转角∠ABA′,然后利用弧长公式列式计算即可得解.
解答 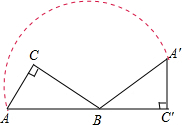 解:在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$cm,
解:在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$cm,
∴∠ABC=30°,AB=2$\sqrt{3}$,∠ABA′=150°,
根据弧长公式L=$\frac{nπr}{180}$=150×π×2$\sqrt{3}$÷180=$\frac{5\sqrt{3}}{3}$,
故选B.
点评 本题考查了旋转的性质,直角三角形两锐角互余,直角三角形30°角所对的直角边等于斜边的一半的性质,弧长公式,熟记各性质是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
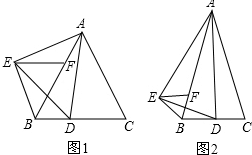
 将三个三角形(△ABC、△ACD、△ADE)拼接在一起恰巧组成∠BAE=90°,AB=AE,已知BC=3,DE=2,∠B=∠E=90°,∠CAD=45°,则CD长为5.
将三个三角形(△ABC、△ACD、△ADE)拼接在一起恰巧组成∠BAE=90°,AB=AE,已知BC=3,DE=2,∠B=∠E=90°,∠CAD=45°,则CD长为5.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,把一个长方形的纸片按图示对折两次,然后剪下一部分,为了得到一个钝角为100°的菱形,剪口与第二次折痕所成角的度数应为( )
如图,把一个长方形的纸片按图示对折两次,然后剪下一部分,为了得到一个钝角为100°的菱形,剪口与第二次折痕所成角的度数应为( )| A. | 30°或50° | B. | 30°或60° | C. | 40°或50° | D. | 40°或60° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
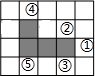 如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )
如图,在方格纸中,随机选择标有序号①②③④⑤中的一个小正方形涂黑,与图中阴影部分构成轴对称图形的概率是( )| A. | $\frac{1}{5}$ | B. | $\frac{2}{5}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com