
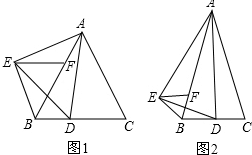
分析 (1)根据已知证明△EAB≌△DAC,得到∠EBA=∠C=60°,根据EF∥BC,得到∠EFB=∠ABC=60°,证明结论;
(2)与(1)的证明过程类似,可以得到答案.
解答 解:(1)△BEF为等边三角形,
∵AB=AC,AD=AE,∠BAC=∠DAE=60°,
∴△AED和△ABC为等边三角形,
∴∠C=∠ABC=60°,∠EAB=∠DAC,
∴△EAB≌△DAC,
∴∠EBA=∠C=60°,
∵EF∥BC,
∴∠EFB=∠ABC=60°,
∵在△EFB中,∠EFB=∠EBA=60°,
∴△EFB为等边三角形,
(2)根据(1)的证明可知,
∠EBA=∠C,∠EFB=∠ABC,
∴△BEF为等腰三角形.
点评 本题考查的是等边三角形和等腰三角形的判定以及三角形全等的判定和性质,灵活运用相关的判定定理和性质定理是解题的关键.


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案科目:初中数学 来源: 题型:解答题
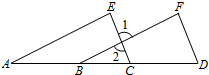 已知:如图,点A,B,C,D在同一直线上,∠F=∠E,DF∥EC.
已知:如图,点A,B,C,D在同一直线上,∠F=∠E,DF∥EC.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
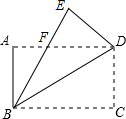 如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.
如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
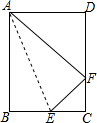 如图,纸片矩形ABCD中,已知:AB=10,AD=8.将AB沿AE折叠,使点B落在边CD的F处,试求:
如图,纸片矩形ABCD中,已知:AB=10,AD=8.将AB沿AE折叠,使点B落在边CD的F处,试求:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
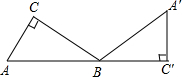 在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )
在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )| A. | $\frac{5}{2}π$ | B. | $\frac{{5\sqrt{3}}}{3}π$ | C. | $\frac{{4\sqrt{3}}}{3}π$ | D. | 2π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
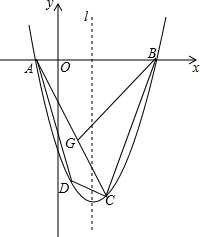 如图,已知二次函数的图象M经过A(-1,0),B(4,0),C(2,-6)三点.
如图,已知二次函数的图象M经过A(-1,0),B(4,0),C(2,-6)三点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com