
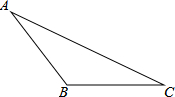
 如图,在△ABC中画出高线AD、中线BE、角平分线CF.
如图,在△ABC中画出高线AD、中线BE、角平分线CF.  学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案 新思维寒假作业系列答案
新思维寒假作业系列答案科目:初中数学 来源: 题型:解答题
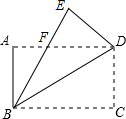 如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.
如图,四边形ABCD是矩形,把矩形沿对角线BD折叠,点C落在点E处,BE与AD相交于点E.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间.
如图,矩形ABCD中,AB=8cm,BC=6cm,动点P从点A出发,以每秒1cm的速度沿线段AB向点B运动,连接DP,把∠A沿DP折叠,使点A落在点A′处.求出当△BPA′为直角三角形时,点P运动的时间.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
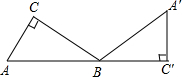 在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )
在Rt△ABC中,∠C=90°,∠A=60°,AC=$\sqrt{3}$,将△ABC绕点B旋转到△A′BC′的位置,且使A、B、C′三点在同一条直线上,则点A经过的最短路线是( )| A. | $\frac{5}{2}π$ | B. | $\frac{{5\sqrt{3}}}{3}π$ | C. | $\frac{{4\sqrt{3}}}{3}π$ | D. | 2π |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图是一张直角三角形的纸片,两直角边AC=6、BC=8,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )
如图是一张直角三角形的纸片,两直角边AC=6、BC=8,现将△ABC折叠,使点B与点A重合,折痕为DE,则BE的长为( )| A. | 4 | B. | 5 | C. | 6 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
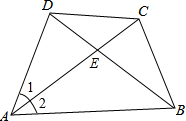 四边形ABCD中,AC为AB、AD的比例中项,且AC平分∠DAB,求证:$\frac{BE}{DE}$=$\frac{B{C}^{2}}{C{D}^{2}}$.
四边形ABCD中,AC为AB、AD的比例中项,且AC平分∠DAB,求证:$\frac{BE}{DE}$=$\frac{B{C}^{2}}{C{D}^{2}}$.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )
今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示.下列说法错误的是( )| A. | 小明中途休息用了20分钟 | |
| B. | 小明休息前爬山的平均速度为每分钟70米 | |
| C. | 小明在上述过程中所走的路程为6600米 | |
| D. | 小明休息前爬山的平均速度大于休息后爬山的平均速度 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com