
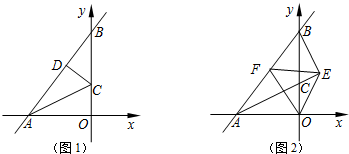
分析 (1)利用待定系数法可直接求得直线AB的解析式,根据A、B的坐标可求得OB、AB、AO,再根据折叠的性质在Rt△BCD中,可求得CD的长,可求得OC的长,可求得C点坐标,由待定系数法可求得直线AC的解析式;
(2)可先证明△ABE∽△ACO,可求得E点坐标,再由内心的性质可证明△AOE≌△AFE,可求得F点坐标,再证明∠FOB=∠EOB即可.
解答 解:
(1)设直线AB解析式为y=kx+b,
把A、B两点坐标代入可得$\left\{\begin{array}{l}{8=b}\\{0=-6k+b}\end{array}\right.$,解得$\left\{\begin{array}{l}{k=\frac{4}{3}}\\{b=8}\end{array}\right.$,
∴直线AB解析式为y=$\frac{4}{3}$x+8;
设C点坐标为(0,x),则OC=CD=x,
又A(-6,0),B(0,8),
∴AO=6,BO=8,AB=10,
∴AD=AO=6,BD=AB-AD=10-6=4,BC=OB-OC=8-x,
在Rt△BCD中,由勾股定理可得BD2+CD2=BC2,
即42+x2=(8-x)2,解得x=3,
∴点C坐标为(0,3),
设直线AC的解析式为y=mx+n,
把A、C坐标代入可得$\left\{\begin{array}{l}{3=n}\\{0=-6m+n}\end{array}\right.$,解得$\left\{\begin{array}{l}{m=\frac{1}{2}}\\{n=3}\end{array}\right.$,
∴直线AC的解析式为y=$\frac{1}{2}$x+3;
(2)由题意可知∠BAE=∠OAC,且∠BEA=∠∠COA=90°,
∴△ABE∽△ACO,
∴$\frac{AB}{AC}$=$\frac{AE}{AO}$,
又由(1)可知AB=10,AC=3$\sqrt{5}$,AO=6,
∴$\frac{10}{3\sqrt{5}}$=$\frac{AE}{6}$,解得AE=4$\sqrt{5}$,
∵E在直线AC上,
∴可设点E坐标为(x,$\frac{1}{2}$x+3),
∴AE=$\sqrt{[x-(-6)]^{2}+(\frac{1}{2}x+3)^{2}}$,
∴$\sqrt{[x-(-6)]^{2}+(\frac{1}{2}x+3)^{2}}$=4$\sqrt{5}$,解得x=2或x=-14(舍去),
∴E点坐标为(2,4),
若C为△EOF的内心,则∠FEA=∠OEA,且∠FAE=∠OAE,
在△AOE和△AFE中
$\left\{\begin{array}{l}{∠AEO=∠FEA}\\{AE=AE}\\{∠OAE=∠FAE}\end{array}\right.$
∴△AOE≌△AFE(ASA),
∴AF=AO=6,
∵点F在直线AB上,
∴可设F点坐标为(a,$\frac{4}{3}$a+8),
∴AF=$\sqrt{[a-(-6)]^{2}+(\frac{4}{3}a+8)^{2}}$=6,解得a=-$\frac{12}{5}$或a=-$\frac{54}{5}$(舍去),
∴F(-$\frac{12}{5}$,$\frac{24}{5}$),
分别过F、E作x轴的垂线,垂足分别为M、N,如图,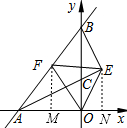
则FM=$\frac{24}{5}$,OM=$\frac{12}{5}$,且NE=4,ON=2,
∴$\frac{FM}{EN}$=$\frac{MO}{ON}$,且∠FMO=∠ENO=90°,
∴△FMO∽△ENO,
∴∠FOM=∠EON,
∴∠FOB=∠EOB,
即OB平分∠FOE,
∴C为△EOF的内心,
综上可知存在点F(-$\frac{12}{5}$,$\frac{24}{5}$),使点C为△EOF的内心.
点评 本题主要考查一次函数的综合应用,涉及知识点有待定系数法、勾股定理、全等三角形的判定和性质、相似三角形的判定和性质、三角形内心的性质等.在(1)中求得点C的坐标是解题的关键,注意方程思想的应用;在(2)中求得E、F的坐标是解题的关键.本题知识点较多,综合性较强,难度适中.


科目:初中数学 来源: 题型:选择题
| A. | $\frac{1}{9}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{2}{9}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 2.5×10-5 | B. | 0.25×10-7 | C. | 2.5×10-6 | D. | 25×10-5 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 四个角相等的四边形是矩形 | B. | 对角线垂直的四边形是菱形 | ||
| C. | 对角线相等的四边形是矩形 | D. | 四边相等的四边形是正方形 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
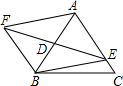 如图,在等边△ABC中,AB=1,D为AB边的中点,E为直线AC上一点,连接ED并延长,在ED的延长线上取点F,使DF=DE,连接AF,BF,BE.
如图,在等边△ABC中,AB=1,D为AB边的中点,E为直线AC上一点,连接ED并延长,在ED的延长线上取点F,使DF=DE,连接AF,BF,BE.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com