练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，一次函数y＝（m+1）x+的图象与x轴的负半轴相交于点A，与y轴相交于点B，且△OAB的面积为．

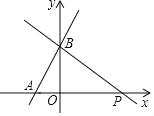
    （1）求m的值及点A的坐标；

    （2）过点B作直线BP与x轴的正半轴相交于点P，且OP＝3OA，求直线BP的解析式．

    【答案】（1），；（2）

    【解析】

    （1）先求得，然后根据三角形面积求得的长，即可求得A的坐标，把它代入y＝（m+1）x+，即可求得m的值；

    （2）根据OP＝3OA，可求出P的坐标，然后用待定系数法求得直线BP的解析式．

    （1）由一次函数y＝（m+1）x+可知：点B(0，)

    OB=

    △OAB的面积为

    把代入y＝（m+1）x+，即（m+1）(－1)+=0，

    解得：m=

    故答案是：，

    （2），

    OP＝3OA＝3，

    P的坐标是，

    设直线BP的解析式为

    把点B(0，)、点P(3，0)代入得

    解得：，b=

    直线BP的解析式为

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】我校图书馆大楼工程在招标时，接到甲乙两个工程队的投标书，每施工一个月，需付甲工程队工程款16万元，付乙工程队12万元。工程领导小组根据甲乙两队的投标书测算，可有三种施工方案：

    （1）甲队单独完成此项工程刚好如期完工；

    （2）乙队单独完成此项工程要比规定工期多用3个月；

    （3）若甲乙两队合作2个月，剩下的工程由乙队独做也正好如期完工。

    你觉得哪一种施工方案最节省工程款，说明理由。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（1）已知关于x的方程2x2﹣mx﹣m2=0有一个根是1，求m的值；

    （2）已知关于x的方程（2x﹣m）（mx+1）=（3x+1）（mx﹣1）有一个根是0，求另一个根和m的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（题文）(1)阅读理解：

    如图1，在△ABC中，若AB＝10，AC＝6，求BC边上的中线AD的取值范围．

    解决此问题可以用如下方法：延长AD到点E使DE＝AD，连接BE(或将△ACD绕着点D逆时针旋转180°得到△EBD，把AB，AC，2AD集中在△ABE中．利用三角形三边的关系即可判断中线AD的取值范围是_________；

    (2)问题解决：

    如图2，在△ABC中，D是BC边上的中点，DE⊥DF于点D，DE交AB于点E，DF交AC于点F，连接EF，求证BE＋CF＞EF.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

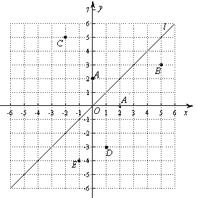
    【题目】如图，在平面直角坐标系中，直线l是第一、三象限的角平分线．

    实验与探究：

    （1）由图观察易知A（0，2）关于直线l的对称点A′的坐标为（2，0），请在图中分别标明B（5，3）、C（﹣2，5）关于直线l的对称点B′、C′的位置，并写出他们的坐标：B′_______、C′_______；

    归纳与发现：

    （2）结合图形观察以上三组点的坐标，你会发现：坐标平面内任一点P（a，b）关于第一、三象限的角平分线l的对称点P′的坐标为________；

    运用与拓展：

    （3）图中在直线l上取一点Q，使Q到D（1，-3），E（-1，-4）两点的距离之和最小，则点Q的坐标是____________。

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线l：y=x+6交x、y轴分别为A、B两点，C点与A点关于y轴对称．动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．

    （1）点A坐标是 ，点B的坐标 ，BC= ．

    （2）当点P在什么位置时，△APQ≌△CBP，说明理由．

    （3）当△PQB为等腰三角形时，求点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图①：要设计一幅宽，长的矩形图案，其中有两横两竖的彩条，横、竖彩条的宽度比为，如果要使所有彩条所占面积为原矩形图案面积的三分之一，应如何设计每个彩条的宽度？

    由横、竖彩条的宽度比为，可设每个横彩条的宽为，则每个竖彩条的宽为．为更好地寻找题目中的等量关系，将横、竖彩条分别集中，原问题转化为如图②的情况，得到矩形．

    结合以上分析完成填空：

    如图②：用含的代数式表示：________；________；矩形的面积为________；列出方程并完成本题解答．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知A（﹣4，2）、B（n，﹣4）两点是一次函数y=kx+b和反比例函数y=图象的两个交点．

    （1）求一次函数和反比例函数的解析式；

    （2）求△AOB的面积；

    （3）观察图象，直接写出不等式kx+b﹣＞0的解集．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：在△ABC中，AC=BC，∠ACB=90°，点D是AB的中点，点E是AB边上一点．

    （1）直线BF垂直于直线CE于点F，交CD于点G（如图1），求证：AE=CG；

    （2）直线AH垂直于直线CE，垂足为点H，交CD的延长线于点M（如图2），找出图中与BE相等的线段，并证明．

    查看答案和解析>>

    同步练习册答案