
【题目】如图,直线l:y=![]() x+6交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.
x+6交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.

(1)点A坐标是 ,点B的坐标 ,BC= .
(2)当点P在什么位置时,△APQ≌△CBP,说明理由.
(3)当△PQB为等腰三角形时,求点P的坐标.
【答案】(1)A的坐标是(﹣8,0),点B的坐标是(0,6),BC=![]() =10,(2)当P的坐标是(2,0)时,△APQ≌△CBP.(3)(﹣8,0),(0,6),10.
=10,(2)当P的坐标是(2,0)时,△APQ≌△CBP.(3)(﹣8,0),(0,6),10.
【解析】
试题分析:(1)把x=0和y=0分别代入一次函数的解析式,求出A、B的坐标,根据勾股定理求出BC即可.
(2)求出∠PAQ=∠BCP,∠AQP=∠BPC,根据点的坐标求出AP=BC,根据全等三角形的判定推出即可.
(3)分为三种情况:①PQ=BP,②BQ=QP,③BQ=BP,根据(2)即可推出①,根据三角形外角性质即可判断②,根据勾股定理得出方程,即可求出③.
解:(1)∵y=![]() x+6
x+6
∴当x=0时,y=6,
当y=0时,x=﹣8,
即点A的坐标是(﹣8,0),点B的坐标是(0,6),
∵C点与A点关于y轴对称,
∴C的坐标是(8,0),
∴OA=8,OC=8,OB=6,
由勾股定理得:BC=![]() =10,
=10,
(2)当P的坐标是(2,0)时,△APQ≌△CBP,
理由是:∵OA=8,P(2,0),
∴AP=8+2=10=BP,
∵∠BPQ=∠BAO,∠BAO+∠AQP+∠APQ=180°,∠APQ+∠BPQ+∠BPC=180°,
∴∠AQP=∠BPC,
∵A和C关于y轴对称,
∴∠BAO=∠BCP,
在△APQ和△CBP中,
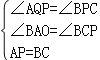 ,
,
∴△APQ≌△CBP(AAS),
∴当P的坐标是(2,0)时,△APQ≌△CBP.
(3)分为三种情况:
①当PB=PQ时,∵由(2)知,△APQ≌△CBP,
∴PB=PQ,
即此时P的坐标是(2,0);
②当BQ=BP时,则∠BPQ=∠BQP,
∵∠BAO=∠BPQ,
∴∠BAO=∠BQP,
而根据三角形的外角性质得:∠BQP>∠BAO,
∴此种情况不存在;
③当QB=QP时,则∠BPQ=∠QBP=∠BAO,
即BP=AP,
设此时P的坐标是(x,0),
∵在Rt△OBP中,由勾股定理得:BP2=OP2+OB2,
∴(x+8)2=x2+62,
解得:x=﹣![]() ,
,
即此时P的坐标是(﹣![]() ,0).
,0).
∴当△PQB为等腰三角形时,点P的坐标是(2,0)或(﹣![]() ,0).
,0).
故答案为:(﹣8,0),(0,6),10.


科目:初中数学 来源: 题型:
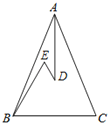
【题目】如图所示,在△ABC中,AB=AC,D,E是△ABC内两点,AD平分∠BAC,∠EBC≡∠E=60°,若BE=10,DE=4,则BC的长度是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】市场上甲种商品的采购价为60元/件,乙种商品的采购价为100元/件,某商店需要采购甲、乙两种商品共15件,且乙种商品的件数不少于甲种商品件数的2倍.设购买甲种商品![]() 件(
件(![]() >0),购买两种商品共花费
>0),购买两种商品共花费![]() 元.
元.
(1)求出![]() 与
与![]() 的函数关系式(写出自变量
的函数关系式(写出自变量![]() 的取值范围);
的取值范围);
(2)试利用函数的性质说明,当采购多少件甲种商品时,所需要的费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,点A(-2,-3),B(1,0),C(3,4),若以A、B、C、D为顶点的四边形是平行四边形,则点D的坐标为__________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=(m+1)x+![]() 的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB的面积为
的图象与x轴的负半轴相交于点A,与y轴相交于点B,且△OAB的面积为![]() .
.
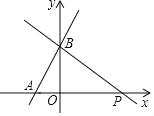
(1)求m的值及点A的坐标;
(2)过点B作直线BP与x轴的正半轴相交于点P,且OP=3OA,求直线BP的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】平面直角坐标系xOy中,点A、B的横坐标分别为a、a+2,二次函数y=﹣x2+(m﹣2)x+2m的图象经过点A、B,且a、m满足2a﹣m=d(d为常数).
(1)若一次函数y1=kx+b的图象经过A、B两点.
①当a=1、d=﹣1时,求k的值;
②若y随x的增大而减小,求d的取值范围;
(2)当d=﹣4且a≠﹣2、a≠﹣4时,判断直线AB与x轴的位置关系,并说明理由;
(3)点A、B的位置随着a的变化而变化,设点A、B运动的路线与y轴分别相交于点C、D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】妈妈在超市购买两种优质水果.先购买了2千克甲水果和3千克乙水果,共花费90元;后又购买了1千克甲水果和2千克乙水果,共花费55元.(每次两种水果的售价都不变)
(1)求甲水果和乙水果的售价分别是每千克多少元;
(2)如果还需购买两种水果共12千克,要求乙水果的数量不少于甲水果数量的2倍,请设计一种购买方案,使所需总费用最低.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).

(1)在图中作出△ABC 关于 y 轴对称的△A1B1C1并写出坐标;
(2)求出△A1B1C1的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com