
【题目】平面直角坐标系xOy中,点A、B的横坐标分别为a、a+2,二次函数y=﹣x2+(m﹣2)x+2m的图象经过点A、B,且a、m满足2a﹣m=d(d为常数).
(1)若一次函数y1=kx+b的图象经过A、B两点.
①当a=1、d=﹣1时,求k的值;
②若y随x的增大而减小,求d的取值范围;
(2)当d=﹣4且a≠﹣2、a≠﹣4时,判断直线AB与x轴的位置关系,并说明理由;
(3)点A、B的位置随着a的变化而变化,设点A、B运动的路线与y轴分别相交于点C、D,线段CD的长度会发生变化吗?如果不变,求出CD的长;如果变化,请说明理由.
【答案】(1)①k的值为﹣3,②d的取值范围为d>﹣4;(2)AB∥x轴.理由见解析;(3)线段CD的长度不变,理由见解析.
【解析】
(1)①当a=1、d=-1时,m=2a-d=3,于是得到抛物线的解析式,然后求得点A和点B的坐标,最后将点A和点B的坐标代入直线AB的解析式求得k的值即可;
②将x=a,x=a+2代入抛物线的解析式可求得点A和点B的纵坐标,然后依据y1随着x的增大而减小,可得到-(a-m)(a+2)>-(a+2-m)(a+4),结合已知条件2a-m=d,可求得d的取值范围;
(2)由d=-4可得到m=2a+4,则抛物线的解析式为y=-x2+(2a+2)x+4a+8,然后将x=a、x=a+2代入抛物线的解析式可求得点A和点B的纵坐标,最后依据点A和点B的纵坐标可判断出AB与x轴的位置关系;
(3)先求得点A和点B的坐标,于是得到点A和点B运动的路线与字母a的函数关系式,则点C(0,2m),D(0,4m-8),于是可得到CD与m的关系式.
(1)①当![]() 时,
时,![]()
所以二次函数的表达式是![]()
∵a=1,
∴点A的横坐标为1,点B的横坐标为3,
把x=1代入抛物线的解析式得:y=6,把x=3代入抛物线的解析式得:y=0,
∴A(1,6),B(3,0).
将点A和点B的坐标代入直线的解析式得:![]() 解得:
解得:![]()
所以k的值为﹣3.
②∵![]()
∴当x=a时,![]() ;当x=a+2时,
;当x=a+2时,![]()
∵y1随着x的增大而减小,且a<a+2,
∴![]() 解得:
解得:![]()
又∵![]()
∴d的取值范围为![]()
(2)∵![]() 且
且![]()
∴m=2a+4.
∴二次函数的关系式为![]()
把x=a代入抛物线的解析式得:y=a2+6a+8.
把x=a+2代入抛物线的解析式得:y=a2+6a+8.
∴A(a,a2+6a+8)、B(a+2,a2+6a+8).
∵点A、点B的纵坐标相同,
∴AB∥x轴.
(3)线段CD的长度不变.
∵![]() 过点A、点B,
过点A、点B,![]() ,
,
∴![]()
∴![]()
∵把a=0代入![]() ,得:
,得:![]()
∴![]()
∵点D在y轴上,即a+2=0,
∴![]()
把![]() 代入
代入![]() 得:
得:![]()
∴![]()
∴![]()
∴线段CD的长度不变.


科目:初中数学 来源: 题型:
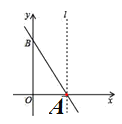
【题目】已知一次函数y=﹣![]() x+
x+![]() 的图象与x轴、y轴分别交于A、B两点.直线l过点A且垂直于x轴.两动点D、E分别从A B两点间时出发向O点运动(运动到O点停止).运动速度分别是每秒1个单位长度和
的图象与x轴、y轴分别交于A、B两点.直线l过点A且垂直于x轴.两动点D、E分别从A B两点间时出发向O点运动(运动到O点停止).运动速度分别是每秒1个单位长度和![]() 个单位长度.点G、E关于直线l对称,GE交AB于点F.设D、E的运动时间为t(s).
个单位长度.点G、E关于直线l对称,GE交AB于点F.设D、E的运动时间为t(s).
(1)当t为何值时,四边形是菱形?判断此时△AFG与AGB是否相似,并说明理由;
(2)当△ADF是直角三角形时,求△BEF与△BFG的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一水果店主分两批购进某一种水果,第一批所用资金为2400元,因天气原因,水果涨价,第二批所用资金是2700元,但由于第二批单价比第一批单价每箱多10元,以致购买的数量比第一批少25%.
(1)该水果店主购进第一批这种水果的单价是多少元?
(2)该水果店主计两批水果的售价均定为每箱40元,实际销售时按计划无损耗售完第一批后,发现第二批水果品质不如第一批,于是该店主将售价下降a%销售,结果还是出现了20%的损耗,但这两批水果销售完后仍赚了不低于1716元,求a的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校园文学社为了解本校学生对本社一种报纸四个版面的喜欢情况,随机抽取部分学生做了一次问卷调查,要求学生选出自己喜欢的一个版面,将调查数据进行了整理、绘制成部分统计图如下:
各版面选择人数的扇形统计图 各版面选择人数的条形统计图


请根据图中信息,解答下列问题:
(1)该调查的样本容量为 ,![]()
![]() ,“第一版”对应扇形的圆心角为
,“第一版”对应扇形的圆心角为 ![]() ;
;
(2)请你补全条形统计图;
(3)若该校有![]() 名学生,请你估计全校学生中最喜欢“第一版”的人数.
名学生,请你估计全校学生中最喜欢“第一版”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l:y=![]() x+6交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.
x+6交x、y轴分别为A、B两点,C点与A点关于y轴对称.动点P、Q分别在线段AC、AB上(点P不与点A、C重合),满足∠BPQ=∠BAO.

(1)点A坐标是 ,点B的坐标 ,BC= .
(2)当点P在什么位置时,△APQ≌△CBP,说明理由.
(3)当△PQB为等腰三角形时,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将半径为2,圆心角为120°的扇形OAB绕点A逆时针旋转60°,点O,B的对应点分别为O′,B′,连接BB′,则图中阴影部分的面积是( )

A. ![]() B. 2
B. 2![]() -
-![]() C. 2
C. 2![]() -
-![]() D. 4
D. 4![]() -
-![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为弘扬中华传统文化,某校举办了学生“国学经典大赛”.比赛项目为:![]() .唐诗;
.唐诗;![]() .宋词;
.宋词;![]() .论语;
.论语;![]() .三字经.比赛形式分“单人组”和“双人组”.
.三字经.比赛形式分“单人组”和“双人组”.
(1)小丽参加“单人组”,她从中随机抽取一个比赛项目,恰好抽中“三字经”的概率是多少?
(2)小红和小明组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则小红和小明都没有抽到“论语”的概率是多少?请用画树状图或列表的方法进行说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AC,BE⊥AC于点E,CF⊥AB于点F,BE与CF交于点D,则下列结论中不正确的是( )
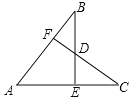
A. ![]() B.
B. ![]() C. 点D在
C. 点D在![]() 的平分线上D. 点D是CF的中点
的平分线上D. 点D是CF的中点
查看答案和解析>>
科目:初中数学 来源: 题型:
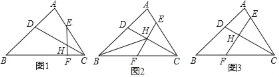
【题目】△ABC中,BC>AC,CD平分∠ACB交于AB于D,E,F分别是AC,BC边上的两点,EF交于CD于H,
(1)如图1,若∠EFC=∠A,求证:CECD=CHBC;
(2)如图2,若BH平分∠ABC,CE=CF,BF=3,AE=2,求EF的长;
(3)如图3,若CE≠CF,∠CEF=∠B,∠ACB=60°,CH=5,CE=4![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com