【题目】如图，已知
，点
、
、
、…在射线ON上，点
、
、
、…在射线OM上，
、
、
…均为等边三角形，若
，则
的边长为( )
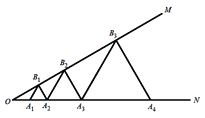
A.16B.64C.128D.256
【答案】C
【解析】
根据等腰三角形的性质以及平行线的性质得出A1B1∥A2B2∥A3B3，以及A2B2=2B1A2，得出A3B3=4B1A2=4，A4B4=8B1A2=8，A5B5=16B1A2…进而得出答案．
如图，
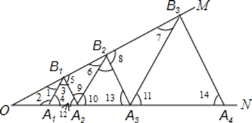
∵△A1B1A2是等边三角形，
∴A1B1=A2B1，∠3=∠4=∠12=60°，
∴∠2=120°，
∵∠MON=30°，
∴∠1=180°-120°-30°=30°，
又∵∠3=60°，
∴∠5=180°-60°-30°=90°，
∵∠MON=∠1=30°，
∴OA1=A1B1=1，
∴A2B1=1，
∵△A2B2A3、△A3B3A4是等边三角形，
∴∠11=∠10=60°，∠13=60°，
∵∠4=∠12=60°，
∴A1B1∥A2B2∥A3B3，B1A2∥B2A3，
∴∠1=∠6=∠7=30°，∠5=∠8=90°，
∴A2B2=2B1A2，B3A3=2B2A3，
∴A3B3=4B1A2=4，
A4B4=8B1A2=8，
A5B5=16B1A2=16，
以此类推：A8B8=27B1A2=27=128．
故选C．
阅读快车系列答案科目：初中数学 来源： 题型：
【题目】如图，直线l：y=
x+6交x、y轴分别为A、B两点，C点与A点关于y轴对称．动点P、Q分别在线段AC、AB上（点P不与点A、C重合），满足∠BPQ=∠BAO．
（1）点A坐标是 ，点B的坐标 ，BC= ．
（2）当点P在什么位置时，△APQ≌△CBP，说明理由．
（3）当△PQB为等腰三角形时，求点P的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】法国数学家柯西于1813年在拉格朗日、高斯的基础上彻底证明了《费马多边形数定理》，其主要突破在“五边形数”的证明上．如图为前几个“五边形数”的对应图形，请据此推断，第10个“五边形数”应该为（ ），第2018个“五边形数”的奇偶性为（ ）
A. 145；偶数 B. 145；奇数 C. 176；偶数 D. 176；奇数
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】已知：在△ABC中，AC=BC，∠ACB=90°，点D是AB的中点，点E是AB边上一点．
（1）直线BF垂直于直线CE于点F，交CD于点G（如图1），求证：AE=CG；
（2）直线AH垂直于直线CE，垂足为点H，交CD的延长线于点M（如图2），找出图中与BE相等的线段，并证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】△ABC中，BC＞AC，CD平分∠ACB交于AB于D，E，F分别是AC，BC边上的两点，EF交于CD于H，
（1）如图1，若∠EFC=∠A，求证：CECD=CHBC；
（2）如图2，若BH平分∠ABC，CE=CF，BF=3，AE=2，求EF的长；
（3）如图3，若CE≠CF，∠CEF=∠B，∠ACB=60°，CH=5，CE=4
，求
的值．
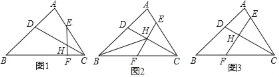
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】某公司举行周年庆典，决定订购一批印有公司logo的记事本赠送给客户，购买甲种记事本共花费3000元，购买乙种记事本共花费2100元，购买甲种记事本的数量是购买乙种记事本数量的2倍，且购买一个乙种记事本比购买一个甲种记事本多花20元.
(1)求购买一个甲种记事本，一个乙种记事本各需多少元？
(2)由于公司业务的扩大，公司决定再次购买甲、乙两种记事本共40个，且乙种记事本不少于23个，预算金额不超过2400元，购买时恰逢该店对两种记事本的售价进行调整，甲种记事本售价比第一次购买时提高了10%，乙种记事本售价比第一次购买时降低了10%，请问该公司有哪几种方案购买这批记事本？
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】如图，在
中，
为锐角，点
为射线
上一动点，连接
.以为直角边且在的上方作等腰直角三角形
.
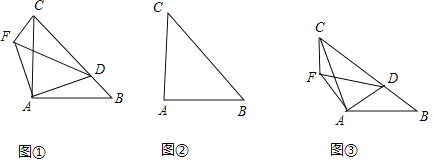
（1）若
，
①当点在线段上时（与点
不重合），试探讨
与
的数量关系和位置关系；
②当点在线段
的延长线上时，①中的结论是否仍然成立，请在图2中面出相应的图形并说明理由；
（2）如图3，若
，
，
，点在线段上运动，试探究与的位置关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
