
【题目】如图,在![]() 中,
中,![]() 为锐角,点
为锐角,点![]() 为射线
为射线![]() 上一动点,连接
上一动点,连接![]() .以
.以![]() 为直角边且在
为直角边且在![]() 的上方作等腰直角三角形
的上方作等腰直角三角形![]() .
.
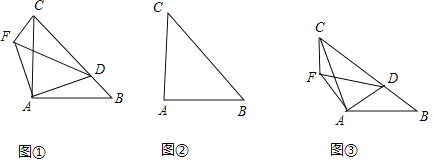
(1)若![]() ,
,![]()
①当点![]() 在线段
在线段![]() 上时(与点
上时(与点![]() 不重合),试探讨
不重合),试探讨![]() 与
与![]() 的数量关系和位置关系;
的数量关系和位置关系;
②当点![]() 在线段
在线段![]() 的延长线上时,①中的结论是否仍然成立,请在图2中面出相应的图形并说明理由;
的延长线上时,①中的结论是否仍然成立,请在图2中面出相应的图形并说明理由;
(2)如图3,若![]() ,
,![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上运动,试探究
上运动,试探究![]() 与
与![]() 的位置关系.
的位置关系.
【答案】(1)①CF⊥BD,证明见解析;②成立,理由见解析;(2)CF⊥BD,证明见解析.
【解析】
(1)①根据同角的余角相等求出∠CAF=∠BAD,然后利用“边角边”证明△ACF和△ABD全等,②先求出∠CAF=∠BAD,然后与①的思路相同求解即可;
(2)过点A作AE⊥AC交BC于E,可得△ACE是等腰直角三角形,根据等腰直角三角形的性质可得AC=AE,∠AED=45°,再根据同角的余角相等求出∠CAF=∠EAD,然后利用“边角边”证明△ACF和△AED全等,根据全等三角形对应角相等可得∠ACF=∠AED,然后求出∠BCF=90°,从而得到CF⊥BD.
解:(1)①∵∠BAC=90°,△ADF是等腰直角三角形,
∴∠CAF+∠CAD=90°,∠BAD+∠ACD=90°,
∴∠CAF=∠BAD,
在△ACF和△ABD中,
∵AB=AC,∠CAF=∠BAD,AD=AF,
∴△ACF≌△ABD(SAS),
∴CF=BD,∠ACF=∠ABD=45°,
∵∠ACB=45°,
∴∠FCB=90°,
∴CF⊥BD;
②成立,理由如下:如图2:
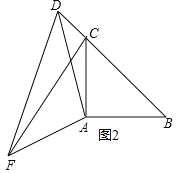
∵∠CAB=∠DAF=90°,
∴∠CAB+∠CAD=∠DAF+∠CAD,
即∠CAF=∠BAD,
在△ACF和△ABD中,
∵AB=AC,∠CAF=∠BAD,AD=AF,
∴△ACF≌△ABD(SAS),
∴CF=BD,∠ACF=∠B,
∵AB=AC,∠BAC=90°,
∴∠B=∠ACB=45°,
∴∠BCF=∠ACF+∠ACB=45°+45°=90°,
∴CF⊥BD;
(2)如图3,过点A作AE⊥AC交BC于E,

∵∠BCA=45°,
∴△ACE是等腰直角三角形,
∴AC=AE,∠AED=45°,
∵∠CAF+∠CAD=90°,∠EAD+∠CAD=90°,
∴∠CAF=∠EAD,
在△ACF和△AED中,
∵AC=AE,∠CAF=∠EAD,AD=AF,
∴△ACF≌△AED(SAS),
∴∠ACF=∠AED=45°,
∴∠BCF=∠ACF+∠BCA=45°+45°=90°,
∴CF⊥BD.


科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,A(1,2),B(3,1),C(-2,-1).

(1)在图中作出△ABC 关于 y 轴对称的△A1B1C1并写出坐标;
(2)求出△A1B1C1的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系中的位置如图所示.
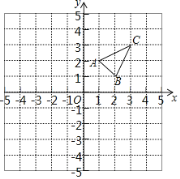
(1)作出与△ABC关于x轴对称的△A1B1C1;
(2)将△ABC向左平移4个单位长度,画出平移后的△A2B2C2;
(3)若在如图的网格中存在格点P,使点P的横、纵坐标之和等于点C的横、纵坐标之和,请写出所有满足条件的格点P的坐标(C除外).
查看答案和解析>>
科目:初中数学 来源: 题型:
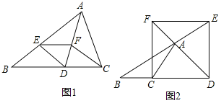
【题目】![]() 如图
如图![]() ,
,![]() 中,
中,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,在
,在![]() 上截取
上截取![]() ,过点
,过点![]() 作
作![]() 交
交![]() 于点
于点![]() .求证:四边形
.求证:四边形![]() 是菱形;
是菱形;
![]() 如图
如图![]() ,
,![]() 中,
中,![]() 平分
平分![]() 的外角
的外角![]() 交
交![]() 的延长线于点
的延长线于点![]() ,在
,在![]() 的延长线上截取
的延长线上截取![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .四边形
.四边形![]() 还是菱形吗?如果是,请证明;如果不是,请说明理由.
还是菱形吗?如果是,请证明;如果不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】湘一“追逐梦想”数学兴趣小组编了一个“诗·远方”的计算程序,规定:输入数据![]() ,
,![]() 时,若输出的是代数式称为“诗
时,若输出的是代数式称为“诗![]() ”,若输出的是等式称为“远方
”,若输出的是等式称为“远方![]() ”.
”.
回答下列问题:
(1)当输入正整数![]() ,
,![]() 时,得到“远方
时,得到“远方![]() ”和“诗
”和“诗![]() ”,若“远方
”,若“远方![]() ”为
”为![]() ,求证“诗
,求证“诗![]() ”:
”:![]() 是完全平方式.(温馨提示:对于一个整式
是完全平方式.(温馨提示:对于一个整式![]() ,如果存在另一个整式
,如果存在另一个整式![]() ,使
,使![]() 的条件,则称
的条件,则称![]() 是完全平方式,比如
是完全平方式,比如![]() ,
,![]() 是完全平方式.)
是完全平方式.)
(2)当输入![]() ,
,![]() 时,求“远方
时,求“远方![]() ”:
”:![]() 的
的![]() ,
,![]() 的正整数解.
的正整数解.
(3)若正数![]() ,
,![]() 互为倒数,求“诗
互为倒数,求“诗![]() ”:
”:![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“鄂尔多斯,温暖全世界”这句广告语及上乘的质量使鄂尔多斯的羊绒制品闻名中外,我市某羊绒企业的工厂店在销售中发现:某种羊绒围巾平均每天可售出![]() 件,每件可获利
件,每件可获利![]() 元;若售价减少
元;若售价减少![]() 元,平均每天就可多售出
元,平均每天就可多售出![]() 件;若想平均每天销售这种围巾盈利
件;若想平均每天销售这种围巾盈利![]() 元,并使顾客得到更大的实惠,那么每件围巾应降价多少元?若想获利最大,应降价多少?
元,并使顾客得到更大的实惠,那么每件围巾应降价多少元?若想获利最大,应降价多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器超市销售A B两种型号的电风扇,A型号每台进价为200元,B型号每台进价分别为150元,下表是近两天的销售情况:
销售时段 | 销售数量 | 销售收入 | |
A种型号 | B种型号 | ||
第一天 | 3台 | 5台 | 1620元 |
第二天 | 4台 | 10台 | 2760元 |
(进价、售价均保持不变,利润=销售收入-进货成本)
(1)求A、B两种型号的电风扇的销售单价;
(2)若超市准备用不多于5400元的金额再采购这两种型号的电风扇共30台,求A种型号的电风扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电风扇能否实现利润不少于1060元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com